Técnica de Graficación de Funciones
En matemáticas, la gráfica de una función es
un tipo de representación gráfica que permite conocer intuitivamente el
comportamiento de dicha función. Más formalmente dada una función:

el gráfico es el conjunto de todos los pares ordenados (x, f(x))
de la función f, es decir, como un subconjunto del producto
cartesiano X×Y. Se representa gráficamente mediante
una correspondencia entre los elementos del conjunto dominio y
los del conjunto imagen.
Las únicas funciones que se pueden trazar de forma no
ambigua mediante líneas, son las de una sola variable, con un sistema de coordenadas
cartesianas, donde cada abscisa representa un valor de la variable del
dominio y cada ordenada representa el valor correspondiente del conjunto
imagen. Si la función es continua, entonces la gráfica formará una línea
recta o curva. En el caso de funciones de dos variables es
posible visualizarlas de forma unívoca mediante una proyección geométrica, pero
a partir de tres variables tan solo es posible visualizar cortes (con un plano)
de la función para los que los valores de todas las variables, excepto dos,
permanezcan constantes. Algunos software de representación usan además colores,
o curvas de nivel lo cual se puede lograr una
representación satisfactoria.
El concepto de gráfica de una función se generaliza a
la gráfica de una relación. Notar que si bien cada función tiene
una única representación gráfica, pueden existir varias funciones que tengan la
misma, pero con dominios y codominios diferentes.
Mediante una gráfica conocida es posible obtener nuevas
gráficas que tengan alguna relación con ella. Estas relaciones matemáticamente
se las representa mediante sumas o productos de constantes con las variables
del dominio y rango de la función original.
Sea y = f(x) una función. Para representarla gráficamente hay que seguir los pasos siguientes:
- Calculo del dominio:
dom(f) = {x ∈ R : ∃f(x)}
- Simetrías
f(−x) = f(x), ∀x ∈ dom(f) ⇐⇒ f es par
f(−x) = −f(x), ∀x ∈ dom(f) ⇐⇒ f es impar
- Corte con los ejes coordenados
La grafica de la funcion y = f(x) cortara al eje de abcisas o eje OX en un punto x0 ∈ dom(f) si
f(x0) = 0, y cortar´a al eje de ordenadas o eje OY si 0 ∈ dom(f).

Asıntotas:
Las asıntotas pueden ser de tres tipos:
Verticales.- La recta x = a es una asıntota vertical de f si

siendo a /∈ dom(f), por lo que la curva jamas cortar´a a dicha asıntota.
Horizontales.- La recta y = b es una asıntota horizontal de f si

Oblicuas.- La recta y = mx + n es una asıntota oblicua de f si

Es fundamental tener en cuenta que si f posee asıntotas horizontales entonces no tendrá asıntota
oblicua alguna.
Máximos y mínimos . Intervalos de crecimiento y decrecimiento.
Para hallar los máximos y mínimos de la función y = f(x) , en primer lugar, debe resolverse la ecuación:
f '(x) = 0
una vez halladas estas raíces (x=a, x=b, ...) junto a aquellos puntos (x=r, x=s, ...) en los que no existe f '(x) deben ser estudiados uno a uno cada caso, pues para ellos hay las siguientes posibilidades:
1) Punto de inflexión: Sea x=a, si f ''(a)=0 y la siguiente derivada, f '''(a) 0, entonces en x=a hay un punto de inflexión (ver la sección 8.6).
0, entonces en x=a hay un punto de inflexión (ver la sección 8.6).
2) Punto extremo (máximo o mínimo): Sea x=a, si f ''(a) 0, entonces en x=a hay un extremo, si máximo o mínimo lo sabremos por el signo de este f ''(a):
0, entonces en x=a hay un extremo, si máximo o mínimo lo sabremos por el signo de este f ''(a):
I) Si f ''(a)>0, entonces en x=a hay un máximo local, cuya magnitud es de f(a).
II) Si f ''(a)<0, entonces en x=a hay un mínimo local, cuya magnitud es de f(a).
En ocasiones calcular f ''(x) puede llegar a ser una tarea demasiado ardua, por otra parte hemos dicho que pueden haber puntos x=r, x=s, ... en los que ni siquiera existe f ' para ellos, en estas situaciones puede realizarse un estudio del rango de crecimiento y decrecimiento de la función f(x).
* Rango de crecimiento: la zona con f '(x) positiva.
* Rango de decrecimiento: la zona con f '(x) negativa.
La forma de realizar este estudio del crecimiento y decrecimiento es tomar los intervalos entre dos puntos de la lista de arriba (a, b), (b, c), ..., y estudiar el signo de f ' en cada zona. Por ejemplo, si en (a, b) la función es creciente y en (b, c) la función es decreciente, en x=b habrá un máximo local, siempre que exista f(b).
Puntos de inflexión. concavidad y convexidad.
Este estudio se realiza sobre la derivada segunda de la función, f ''(x). En primer lugar hallamos las raíces de f ''(x), es decir resolvemos la ecuación:
f ''(x) = 0
tomando las raíces halladas (supongamos que sean r, s, ...) , a las que podemos añadir los puntos en que no existe f ' ó f '', consideramos los intervalos comprendidos entre cada pareja sucesiva de ellas, (r, s), (s, t), ... estudiando el signo de f '' rn cada intervalo. En las zonas en que f ''(x)>0 la curva es cóncava (curva con "concavidad en U"), mientras que en las zonas en que f ''(x)<0 la curva es convexa (curva con "concavidad en  "). Los puntos en los que f ''(x)=0 pueden ser puntos de inflexión (puntos en que cambia la concavidad).
"). Los puntos en los que f ''(x)=0 pueden ser puntos de inflexión (puntos en que cambia la concavidad).
En la gráfica de la figura 1, la función y = f(x) tiene un punto de inflexión en el punto x=s, en el cual la concavidad pasa de "cóncava" a "convexa". En cambio, la función de la figura 2, el punto x=s (un punto en el que f ' no existe) es llamado "punto de retorno", la concavidad a su izquierda y a su derecha es la misma.
EJERCICIOS RESUELTOS
EJEMPLO 1: Hacer un estudio de la gráfica de la función:
Solución: Seguiremos por orden los puntos que hemos indicado.
1. Campo de existencia: El denominador, 1 + x², no se anula en ningún punto, por tanto el campo de existencia es todo R.
2. Simetrías: La función es antisimétrica, puesto que:
3. Corte con los ejes: Para x = 0, tenemos que y = 0. Y si hacemos y = 0, encontramos que la única solución es y=0. En definitiva, hay un solo punto de corte, esto es el (0,0), el orígen.
4. Asíntotas: En cuanto a las asíntotas horizontales podemos hallar los límites:
lo cual nos indica que el eje x=0 es una asíntota horizontal (tanto por la derecha como por la izquierda).
Para las asíntotas verticales vemos dónde se hace infinita la función, y en realidad no hay ningúna, pues no hay ningún valor de x que anule el denominador.
Tampoco existe asíntota oblicua debido a la existencia de una asíntota horizontal.
5. Máximos y mínimos. Crecimiento y decrecimiento: Calculamos la primera derivada de f(x):
la igualamos a 0, f '(x) = 0, y resolvemos la ecuación resultante:
cuyas raíces son x = -1, x = +1. Estos dos puntos son los dos posibles extremos locales, conviene apuntar la magnitud de la función en cada uno de estos puntos:
f(-1) = -1/2 , f(+1) = 1/2
Por otra parte, podemos estudiar si son máximos o mínimos haciendo la derivada segunda de f:
En concreto tenemos, f ''(-1) >0, lo que nos indica que en x=-1 hay un mínimo. Mientras que f ''(-1) <0, lo que significa que en x=+1 hay un máximo.
También podemos hacer un estudio del crecimiento y decrecimiento de la gráfica, estudiando el signo de f ' en las tres regiones (- ,-1), (-1,+1), (+1,+
,-1), (-1,+1), (+1,+ ):
):
(- ,-1) : f '(x) < 0 . La función es decreciente.
,-1) : f '(x) < 0 . La función es decreciente.
(-1,+1) : f '(x) > 0 . La función es creciente.
(+1,+ ): f '(x) < 0 . La función es decreciente.
): f '(x) < 0 . La función es decreciente.
6. Concavidad y puntos de inflexión. Hacemos f ''(x) = 0, y hallamos sus raíces:
Estos tres puntos: x= 0, x = - , x = +
, x = + son precisamente los puntos de inflexión de la curva, allí donde la concavidad cambia de tipo. Finalmente la concavidad la estudiamos en estas cuatro regiones, de acuerdo con el signo de f '':
son precisamente los puntos de inflexión de la curva, allí donde la concavidad cambia de tipo. Finalmente la concavidad la estudiamos en estas cuatro regiones, de acuerdo con el signo de f '':
(- ,-
,- ) : f ''(x) < 0 . La curva es convexa (concavidad en
) : f ''(x) < 0 . La curva es convexa (concavidad en  ).
).
(- , 0) : f ''(x) < 0 . La curva es concava (concavidad en U).
, 0) : f ''(x) < 0 . La curva es concava (concavidad en U).
(0, + ) : f ''(x) < 0 . La curva es convexa (concavidad en
) : f ''(x) < 0 . La curva es convexa (concavidad en  ).
).
(+ , +
, + ) : f ''(x) < 0 . La curva es concava (concavidad en U).
) : f ''(x) < 0 . La curva es concava (concavidad en U).
Reuniendo todos los datos obtenidos podemos pasar a trazar la gráfica de la función:
EJEMPLO 2: Hacer un estudio de la gráfica de la función:
Solución: Seguiremos por orden los puntos que hemos indicado.
1. Campo de existencia: El denominador, x+1, se anula únicamente en el punto x = -1, por lo tanto el campo de existencia será todo R excepto el x= -1.
2. Simetrías: Para comprobarlo hacemos:
consecuentemente, la gráfica no será ni simétrica ni antisimétrica.
3. Corte con los ejes: Hacemos primeramente x = 0 y hallamos "y", luego hacemos y=0 y hallamos x:
Los cortes con los ejes son dos: (0,1) y (1,0).
4. Asíntotas: Para hallar las posibles asíntotas horizontales hacemos los límites en el infinito de x:
que éste límite sea infinito nos indica la no existencia de asíntotas horizontales.
Para las asíntotas verticales tomamos los puntos que hagan infinita la función, en este caso exsite una de ellas:
x = 1
Asíntota oblicua: Se trata de una recta, y = m x + b, cuyos valores m y b son:
por tanto, la asíntota oblicua es la recta: y = x - 3; la cual en forma segmentaria es:
5. Máximos y mínimos. Crecimiento y decrecimiento: Calculamos la primera derivada de f(x):
igualamos a 0 y resolvemos la ecuación:
Hacemos la segunda derivada de la función, tras simplificarla tenemos:
entonces podemos comprobar: f ''(1)>0, lo cual nos indica que la función tiene un mínimo en x=1, es decir el punto (1,0), mientras que f ''(-3)<0 , o sea, f(x) tiene un máximo en x=-3, el punto (-3,-8).
Para estudiar crecimiento y decrecimiento, observamos:
(- ,-3) : f '(x) > 0 . La función es creciente.
,-3) : f '(x) > 0 . La función es creciente.
(-3,-1) : f '(x) < 0 . La función es decreciente.
(-1,+1) : f '(x) < 0 . La función es decreciente.
(+1,+ ): f '(x) > 0 . La función es creciente.
): f '(x) > 0 . La función es creciente.
6. Concavidad y puntos de inflexión. Hacemos f ''(x) = 0, y hallamos sus raíces:
ecuación que no tiene ninguna raíz, lo que nos indica que en la gráfica no hay ningún punto de inflexión. No obstante, debemos estudiar la concavidad de la curva en las regiones (- ,-1), (-1,+
,-1), (-1,+ ):
):
(- ,-1) : f ''(x) < 0 . Concavidad en forma
,-1) : f ''(x) < 0 . Concavidad en forma  .
.
(-1,+ ): f ''(x) > 0 . Concavidad en forma U.
): f ''(x) > 0 . Concavidad en forma U.
Con todo esto podemos pasar a esbozar la gráfica de la función.
EJEMPLO 3: Hacer un estudio de la gráfica de la función:
(por "log x" nos referimos al "logaritmo neperiano" de x)
1. Campo de existencia: Sólo tienen sentido los logaritmos de los números positivos, por tanto el campo de existencia de esta función es la zona positiva de R.
2. Simetrías: Esta función no tiene simetría puesto que no está definida en la zona negativa del eje x.
3. Corte con los ejes: Hacemos primeramente x = 0 y nos queda:
y = (log 0) / 0
un valor que no existe, por tanto la curva no corta al eje Y. Ahora comprobamos el punto x en el que y=0,éste es el punto:
x = 1
puesto que (log 1)/1 = 0, por tanto, la curva corta al eje X en x=1.
4. Asíntotas: Para hallar la posible asíntota horizontal hacemos:
es decir, y = 0, es una asíntota horizontal.
Podemos comprobar también que x=0 es una asíntota vertical, pues:
En definitiva, tenemos que el eje OX es asíntota horizontal, y el eje OY es asíntota vertical.
5. Máximos y mínimos. Crecimiento y decrecimiento: Calculamos las derivadas f '(x) y f ''(x):
hacemos f '(x) = 0 , lo cual equivale a:
1 - log x = 0
cuya única raíz es x = e (recuerde que "log x" es el lograrítmo neperiano, tal que log e = 1). Para este valor resulta que f ''(e)<0, por lo tanto se trata de un máximo local.
Para estudiar crecimiento y decrecimiento lo hacemos en las dos regiones (0,e) y (e,+ ):
):
(0,e) : f '(x)>0, la gráfica es creciente.
(e,+ ): f '(x)>0, la gráfica es decreciente.
): f '(x)>0, la gráfica es decreciente.
6. Concavidad y puntos de inflexión. Hacemos f ''(x) = 0, y hallamos sus raíces:
2 log x - 3 = 0
es decir: log x = 3/2 , cuya solución es x= , representa un punto de inflexión.
, representa un punto de inflexión.
Estudiamos la concavidad en las dos regiones (0, ) y (
) y ( ,+
,+ ):
):
(0, ) : f ''(x)<0, la región es convexa, (concavidad en forma
) : f ''(x)<0, la región es convexa, (concavidad en forma  ).
).
( ,+
,+ ): f ''(x)>0, la región es concava, (concavidad en forma U).
): f ''(x)>0, la región es concava, (concavidad en forma U).
Finalmente pasamos a esbozar la gráfica:
OPERACIONES CON FUNCIONES
Suma de funciones
Sean f y g dos funciones reales de variable real definidas en un mismo intervalo. Se llama suma de ambas funciones, y se representa por f + g, a la función definida por
Resta de funciones
Del mismo modo que se ha definido la suma de funciones, se define la resta de dos funciones reales de variable real f y g, como la función
Para que esto sea posible es necesario que f y g estén definidas en un mismo intervalo.
Producto de funciones
Sean f y g dos funciones reales de variable real, y definidas en un mismo intervalo. Se llama función producto de f y g a la función definida por
Cociente de funciones
Dadas dos funciones reales de variable real, f y g, y definidas en un mismo intervalo, se llama función cociente de f y g a la función definida por
(La función f/g está definida en todos los puntos en los que la función g no se anula.)
Producto de un número por una función
Dado un número real a y una función f, el producto del número por la función es la función definida por
Ejercicios:
Sean las funciones f(x) = 3x + 1, y g(x) = 2x - 4.
Definir la función f + g y calcular las imágenes de los números 2, -3 y 1/5.
Resolución:
· La función f + g se define como
(f + g) (x) = f(x) + g(x) = x + 1 + 2x - 4 = 5x - 3.
· (f + g) (2) = 5 · 2 - 3 = 7
(f + g) (-3) = 5(-3) - 3 = -18
(f + g) (1/5) = 5 · 1/5 - 3 = -2
Obsérvese que si se calculan las imágenes de f y g por separado y se suman, el resultado es el mismo.
Por ejemplo, para la imagen del 2,
‚ Dadas las funciones f (x) = x2 - 3, y g(x) = x + 3, definir la función (f - g)(x).
Calcular las imágenes de 1/3, -2 y 0 mediante la función f - g.
Resolución:
Calculando las imágenes de los números mediante las funciones f y g por separado, y efectuando la resta, se obtiene el mismo resultado.
Resolución:
Calculando las imágenes de los números mediante las funciones f y g por separado, y multiplicando después, se obtienen los mismos resultados.
„ Dadas las funciones f(x) = -x - 1, y g(x) = 2x + 3, definir f/g.
Resolución:
La función f/g está definida para todos los números reales, salvo para x = -3/2, donde la función g se anula.
Calculando por separado las imágenes de los números mediante las funciones f y g, y después efectuando su cociente, se obtienen los mismos resultados.
Obtener las imágenes de los números 2, 1 y 0 mediante la función 3 · f.
Resolución:
FUNCIONES POLINOMIALES
Las funciones polinomiales y su representación gráfica,
tienen gran importancia en la Matemática. Estas funciones son modelos que
describen relaciones entre dos variables que intervienen en diversos problemas
y/o fenómenos que provienen del mundo real.
La función polinomial se llama si porque generalmente su
expresión algebraica es un polinomio; su forma general es:

Como recordaras de tus cursos de álgebra, una expresión
algebraica se puede clasificar por dos características importantes:
a) El número de términos que lo componen
b) El grado de expresión.
Para entender lo anterior, veamos el siguiente ejemplo:

El grado de una función estará dado por el mayor de los exponentes
Gráfica de funciones polinomiales
Propiedades de las funciones polinomiales
1. La gráfica de y = f (x) intercepta al eje Y en
el punto (0,c)
2. La gráfica de y = f (x) intercepta al eje X en
los puntos cuyas abscisas son las raíces de la
ecuación a xn + + a1x + a0 = 0
3. Las funciones polinomiales son funciones continuas.
Entre las funciones polinomiales se encuentran por ejemplo:
las funciones constantes, las
funciones lineales, las funciones cuadráticas, las funciones
cúbicas, cuyas principales
características se describirán a continuación.
FUNCIÓN CONSTANTE
Una función constante es aquella que tiene la
forma y=f(x)=c, donde c es un número real fijo.
El dominio de una función constante es IR, y su recorrido es
{c}. Su gráfica es una rectaparalela (o coincidente) al eje X.

FUNCIÓN LINEAL
Una función lineal es aquella que tiene la forma, o puede
ser llevada a la forma:
y = f (x) = ax + b ,
con a ≠ 0 , a,b∈ IR
Propiedades
1. El gráfico de una función lineal es siempre una línea
recta.
2. El coeficiente a es la pendiente de la recta y=ax+b.
Cuando a>0, la función lineal es creciente, y
cuando a <0, la función lineal esdecreciente.
3. El dominio y el recorrido de una función lineal es IR.
4. La función lineal y = f(x) = ax + b ,
con a ≠ 0 es inyectiva (y sobre), por lo tanto, tiene inversa.
Su inversa es también una función lineal:


Gráfica de y = ax + b , a > 0 Gráfica de y = ax + b , a < 0
Observación. Ecuación general de la recta
La ecuación general de una recta es Ax+By+C=0 con A ≠ 0
o B ≠ 0 .
· Cuando B=0, la
gráfica es una recta paralela al eje Y o coincidente con este eje.
· Cuando B ≠ 0
, la gráfica es una recta que tiene pendiente igual a
Función cuadrática
Una función cuadrática es aquella que tiene la forma, o
puede ser llevada a la forma:
y = f (x) = ax2
+ bx + c , con a ≠ 0 , a,b,c∈ IR
Propiedades de una función cuadrática
1. El gráfico de una función cuadrática es una parábola.
2. La gráfica de y = f (x) = ax2 + bx + c intercepta
al eje Y en el punto (0,c) La gráfica de y = f (x) = ax2 + bx + c intercepta
al eje Xcuando Δ = b2 − 4ac ≥ 0 , y
en tal caso, las abscisas de los puntos de intersección son
las raíces de la ecuación
ax2 + bx + c = 0.
3. Su gráfica es una parábola cuyo vértice es el punto
4. La recta vertical es una recta eje de simetría de su gráfico.
5. Si a>0 la parábola se abre hacia arriba, y si a<0 se abre
hacia abajo.
Gráfica de una función cuadrática
y = f (x) = ax2 + bx + c



a > 0 , Δ > 0
a > 0 , Δ = 0
a> 0 , Δ < 0



a < 0, Δ > 0
a < 0, Δ = 0
a < 0, Δ <0
Función cúbica
Una función cúbica es aquella que tiene la forma,
o puede ser llevada a la forma:
y = f (x) = ax3 + bx2 + cx + d ,
con a ≠ 0 , a,b,c,d ∈ IR
Un ejemplo de función cúbica es la función y = f (x)
= x3 , cuya gráfica es:

Ejercicio
FUNCIÓN RACIONAL
Una función racional f(x) es el cociente de dos polinomios. La palabra racional hace referencia a que esta función es una razón.
P(x) es el polinomio del numerador y Q(x) el del denominador.
El dominio de una función racional son todos los números reales los valores de la variable x que anulan el denominador (Q(x)) = 0), es decir, excepto las raíces del polinomio correspondiente.
La gráfica de estas funciones, si el polinomio del denominador Q(x) es de grado 1, es una hipérbola:
Existen varios casos particulares de funciones racionales:
Funciones de proporcionalidad inversa
El dominio de la función de proporcionalidad inversa es todos los reales menos el 0:
Su gráfica es una hipérbola con asíntotas los ejes de coordenadas X e Y. Su gráfica es simétrica respecto al origen de coordenadas (0,0).
- Si k es positiva, la gráfica estará en el 1º y 3º cuadrante.
- Si k es negativa, la gráfica se situará en el 2º y el 4º cuadrante.
Funciones del tipo (ax+b)/(cx+d)
Son funciones del tipo:
La gráfica de estas funciones también son hipérbolas.
Funciones del tipo k/(x+a)+b
Sean las funciones racionales del tipo:
Estas funciones son iguales que las funciones de proporcionalidad inversa pero trasladadas. En este caso las asíntotas son las rectas paralelas a los ejes x = –a y y = b.
Ejercicio
Función Exponencial
La función exponencial, es conocida formalmente como la función real ex, donde e es el número de Euler, aproximadamente 2.71828.; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=ex o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.
En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma
siendo a, K ∈ R números reales, con a > 0, a ≠ 1. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen.
La función exponencial ex puede ser definida de diversas maneras equivalentes entre sí, como una serie infinita o bien como un límite de una sucesión. En particular puede ser definida como una serie de potencias:
o como el límite de la sucesión:
Propiedades
La función exponencial (y exponenciales en base distinta a e) satisfacen las siguientes propiedades generales.
- Son las únicas funciones que son igual a su derivada (multiplicada por una constante, en el caso de que tengan una base distinta a e)
Derivada
La importancia de las funciones exponenciales en matemática y ciencias radica principalmente de las propiedades de su derivada. En particular,
Es decir, ex es su propia derivada. Es la única función con esa propiedad (sin tomar en cuenta la multiplicación de la función exponencial por una constante). Otras formas de expresar lo anterior:
- La pendiente del gráfico en cualquier punto es la altura de la función en ese punto.
- La razón de aumento de la función en x es igual al valor de la función en x.
- La función es solución de la ecuación diferencial .2
Si la base de la función exponencial es cualquier número real a mayor que 0, entonces su derivada se puede generalizar así:
donde la función ln(a) es el logaritmo natural de a. En el caso particular de a = e resulta que ln(e) = 1 y por lo tanto .
Función exponencial compleja
Como en el caso real, la función exponencial puede ser definida como una función holomorfa en el plano complejode diferentes maneras.3 Algunas de ellas son simples extensiones de las fórmulas que se utilizan para definirla en el dominio de los números reales. Específicamente, la forma más usual de definirla para el dominio de los números complejos es mediante la serie de potencias, donde el valor real x se sustituye por la variable compleja z:
para valores imaginarios puros se cumple la identidad
- ,
en el que un caso particular es la identidad de Euler, conector de números tan importanes como el uno, el cero, e, número pi y la unidad imaginaria.
Usando la identidad anterior, donde ahora z=x+yi, con x e y números reales, se obtiene una definición equivalente a la primera,
ecuación que muestra que esta función, además de ser holomorfa, es periódica, con un periodo para la parte imaginaria de .
EJERCICIOS

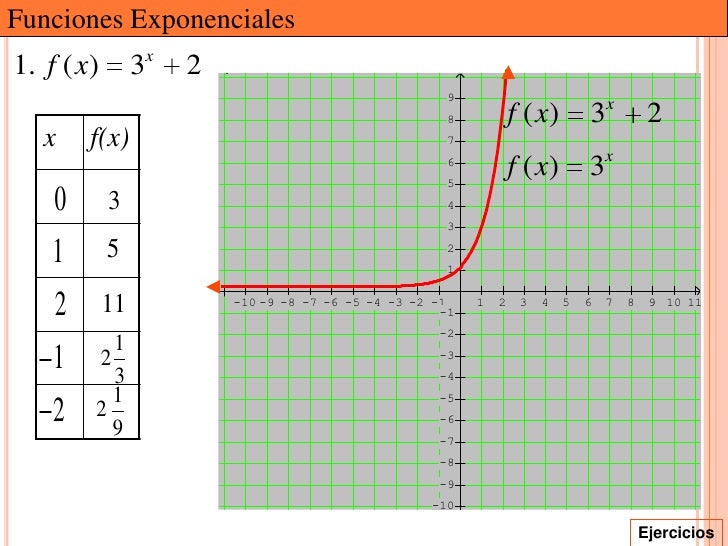
Función Logarítmica
Como la exponencial, la función logarítmica se utiliza con asiduidad en los cálculos y desarrollos de las matemáticas, las ciencias naturales y las ciencias sociales. Entre otros fines, se usa ampliamente para «comprimir» la escala de medida de magnitudes cuyo crecimiento, demasiado rápido, dificulta su representación visual o la sistematización del fenómeno que representa.
Una función logarítmica es aquella que genéricamente se expresa como f (x) == logax, siendo a la base de esta función, que ha de ser positiva y distinta de 1.
La función logarítmica es la inversa de la función exponencial (ver t35), dado que:
loga x = b Û ab = x.
Representación gráfica de funciones logarítmicas y de sus inversas (exponenciales).
Propiedades de la función logarítmica
Las propiedades generales de la función logarítmica se deducen a partir de las de su inversa, la función exponencial. Así, se tiene que:
- La función logarítmica sólo existe para valores de x positivos, sin incluir el cero. Por tanto, su dominio es el intervalo (0,+¥).
- Las imágenes obtenidas de la aplicación de una función logarítmica corresponden a cualquier elemento del conjunto de los números reales, luego el recorrido de esta función es R.
- En el punto x = 1, la función logarítmica se anula, ya que loga 1 = 0, en cualquier base.
- La función logarítmica de la base es siempre igual a 1.
- Finalmente, la función logarítmica es continua, y es creciente para a > 1 y decreciente para a < 1.
Ecuaciones logarítmicas
Cuando en una ecuación la variable o incógnita aparece como argumento o como base de un logaritmo, se llama logarítmica.
La resolución de ecuaciones logarítmicas se basa en los mismos procedimientos utilizados en la resolución de las ecuaciones habituales. Aunque no existen métodos fijos, habitualmente se procura convertir la ecuación logarítmica en otra equivalente donde no aparezca ningún logaritmo. Para ello, se ha de intentar llegar a una situación semejante a la siguiente:
loga f (x) = loga g (x)
Entonces, se emplean los antilogaritmos para simplificar la ecuación hasta f (x) = g (x), que se resuelve por los métodos habituales.
También puede operarse en la ecuación logarítmica para obtener una ecuación equivalente del tipo:
loga f (x) = m
de donde se obtiene que f (x) = am, que sí se puede resolver de la forma habitual.
Sistemas de ecuaciones logarítmicas
Cuando en un sistema aparecen una o varias ecuaciones logarítmicas, se denomina sistema de ecuaciones logarítmicas. En el caso de un sistema de dos ecuaciones con dos incógnitas, se pueden producir tres casos distintos:
- Un sistema formado por una ecuación polinómica y una logarítmica.
- Un sistema constituido por dos ecuaciones logarítmicas.
- Un sistema compuesto por una ecuación polinómica y una ecuación exponencial.
En cada caso, se utilizan los métodos habituales de resolución de sistemas de ecuaciones, teniendo siempre presente que estas ecuaciones han de transformarse en otras equivalentes, donde la incógnita no aparezca en el argumento o la base del logaritmo, ni en el exponente de la función exponencial.
Forma de las funciones logarítmicas según el valor de la base.
Ejemplos
| x | |
|---|---|
| 1/8 | -3 |
| 1/4 | -2 |
| 1/2 | -1 |
| 1 | 0 |
| 2 | 1 |
| 4 | 2 |
| 8 | 3 |
| x | |
|---|---|
| 1/8 | 3 |
| 1/4 | 2 |
| 1/2 | 1 |
| 1 | 0 |
| 2 | −1 |
| 4 | −2 |
| 8 | −3 |


















No hay comentarios:
Publicar un comentario