PROPOSICIONES
Una propocición es el significado de cualquier frase declarativa que pueda ser verdadera o falsa.
Nos referimos a ( v - f ) o (1 - 0) como los valores de verdad.
Ejemplos:
- Hoy es lunes.
- Hablo y no hablo.
- Viene o no viene.
- Carlos Fuentes es un escritor. (Simple)
- Sen(x) no es un número mayor que 1. (Compuesta)
- El 14 y el 7 son factores del 42. (Simple)
Clases de proposiciones
Existen dos clases de proposiciones:
PROPOSICIONES SIMPLES: también denominadas proposiciones atómicas. Son aquellas proposiciones que no se pueden dividir.
Ejemplo:
-
El cielo es azul.
PROPOSICIONES COMPUESTAS: también denominadas moleculares. Son aquellas que están formadas por dos o más proposiciones simples unidas por los operadores lógicos.
Ejemplo:
-
Fui al banco, pero el banco estaba cerrado.
-
Los lectores de este libro son jóvenes o universitarios.
-
Si el miércoles próximo me saco la lotería entonces te regalare un auto.
PROPOSICIONES SIMPLES: también denominadas proposiciones atómicas. Son aquellas proposiciones que no se pueden dividir.
Ejemplo:
- El cielo es azul.
PROPOSICIONES COMPUESTAS: también denominadas moleculares. Son aquellas que están formadas por dos o más proposiciones simples unidas por los operadores lógicos.
Ejemplo:
- Fui al banco, pero el banco estaba cerrado.
- Los lectores de este libro son jóvenes o universitarios.
- Si el miércoles próximo me saco la lotería entonces te regalare un auto.
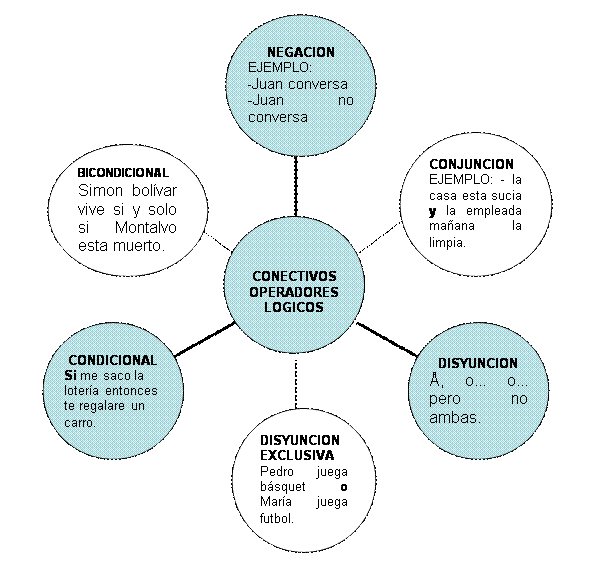
Operadores Lógicos
Los conectivos lógicos son símbolos usados para combinar proposiciones simples, dadas, llamadas proposiciones
Los conectivos lógicos son símbolos usados para combinar proposiciones simples, dadas, llamadas proposiciones
Los conectivos lógicos son:
- ~ negación
- disyunción
- conjunción
- condicionante
- bicondicionante
Los conectivos lógicos son:
- ~ negación
- disyunción
- conjunción
- condicionante
- bicondicionante
Negación
La negación de una proposición es una nueva proposición que tiene un valor de verdad opuesto a la proposición original. Es decir, si el valor de verdad de una proposición p es verdadero, entonces el valor de verdad de ~p es falso.
La tabla de verdad para el conectivo ~ está dada por
p ~p V
F
F
V
Disyunción
La disyunción es la proposición compuesta que resulta de conectar dos proposiciones, p y q, mediante el conectivo .
Esta proposición compuesta de denota por y se lee p o q.
La tabla de verdad para el conectivo está dada por
p q V V
V
V F
V
F V
V
F F
F
Se puede ver que para que una proposición compuesta tenga valor de verdad verdadero, basta con una de las proposiciones simples tenga valor de verdad verdadero.
Conjunción
La conjunción es la proposición compuesta que resulta de conectar dos proposiciones, p y q, mediante el conectivo .
Esta proposición compuesta de denota por y se lee p y q.
La tabla de verdad para el conectivo está dada por
p q V V
V
V F
F
F V
F
F F
F
Se puede ver que para que una proposición compuesta tenga valor de verdad verdadero, ambas proposiciones simples deben tener valor de verdad verdadero.
Condicional
La condicional es la proposición compuesta que resulta de conectar dos proposiciones, p y q, mediante el conectivo .
Esta proposición compuesta de denota por y se lee p implica q.
En esta proposición compuesta, la proposición simple p se llama antecedente, mientras que la proposición simple q se llama consecuente.
La tabla de verdad para el conectivo está dada por
p q V V
V
V F
F
F V
V
F F
V
Se puede ver que una proposición compuesta tiene valor de verdad falso solamente cuando el antecedente es verdadero y el consecuente es falso. En cualquier otro caso, el valor de verdad de la proposición compuesta es verdadero.
Bicondicional
La bicondicional es la proposición compuesta que resulta de conectar dos proposiciones, p y q, mediante el conectivo .
Esta proposición compuesta se denota por y se lee p si y solo si q.
La tabla de verdad para el conectivo está dada por
p q V V
V
V F
F
F V
F
F F
V
Se puede ver que la proposición compuesta tiene valor de verdad verdadero siempre que las proposiciones simples tienen el mismo valor de verdad. Es cualquier otro caso, la proposición compuesta tiene valor de verdad falso
Propiedades de los Operadores Lógicos
Según el escritor (Carlos, 2005) se denominan también leyes, las leyes que se refieren a este conjunto de operadores vienen expresadas por pares, cada una de ellas es la ley Dual de la otra. Esta propiedad se expresa mediante el siguiente teorema de dualidad: sea x y y variables booleanas expresada con el conjunto de operadores. La expresión dual A es una expresión booleana obtenida de A por el intercambio de la conectividad.
Leyes de asociativa
Leyes de idempotencia
Leyes de acotación
Leyes de absorción
Leyes de involución
Leyes de D´ Morgan
Formas Proposicionales
Se denominan formas proposicionales a las estructuras construidas por variables proposicionales y operadores lógicos.
Tautología:
- Cuando se tienen proposiciones verdaderas para todos los valores de verdad de las variables proposicionales. (Intriago, 2015)
Ejemplos:
- Bésame con besos de tu boca
- Subir arriba
- Salir afuera
- Bajar abajo.
- Vive la vida
- Entrar adentro
Contradicción:
- Cuando se tienen proposiciones falsas para todos los valores de verdad de las variables proposicionales. (Intriago, 2015)
- Son cuando aquellas fórmulas que son falsas para cualquier valoración de símbolos proposicionales que contiene. Las proposiciones dan de resultado negativo. (Tautología, Contradicciones, Contingencias Lógicas - Lógica y su fundamento)
Ejemplos:
No es caro, cuesta mucho dinero.
Contingencia:
- Cuando se tienen proposiciones falsas y verdaderas para todos los valores de verdad de las variables proposicionales. (Intriago, 2015)
- Se refiere a algo que es probable que ocurra, aunque tenga la mayor seguridad al respecto. Por lo tanto, es lo posible o aquello que puede o no concretarse.
Ejemplos:
- Creo que me estoy enfermando.
- Dudo que el niño se duerma.
- Podrías leer este libro.
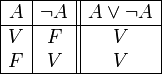
Negación
La negación de una proposición es una nueva proposición que tiene un valor de verdad opuesto a la proposición original. Es decir, si el valor de verdad de una proposición p es verdadero, entonces el valor de verdad de ~p es falso.
La tabla de verdad para el conectivo ~ está dada por
| p | ~p |
|---|---|
| V | |
| F |
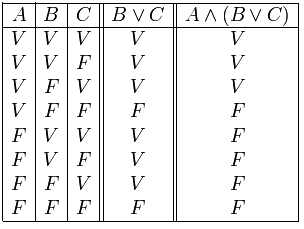
Disyunción
La disyunción es la proposición compuesta que resulta de conectar dos proposiciones, p y q, mediante el conectivo .
Esta proposición compuesta de denota por y se lee p o q.
La tabla de verdad para el conectivo está dada por
| p | q | |
|---|---|---|
| V | V | |
| V | F | |
| F | V | |
| F | F |
Se puede ver que para que una proposición compuesta tenga valor de verdad verdadero, basta con una de las proposiciones simples tenga valor de verdad verdadero.
Conjunción
La conjunción es la proposición compuesta que resulta de conectar dos proposiciones, p y q, mediante el conectivo .
Esta proposición compuesta de denota por y se lee p y q.
La tabla de verdad para el conectivo está dada por
| p | q | |
|---|---|---|
| V | V | |
| V | F | |
| F | V | |
| F | F |
Se puede ver que para que una proposición compuesta tenga valor de verdad verdadero, ambas proposiciones simples deben tener valor de verdad verdadero.
Condicional
La condicional es la proposición compuesta que resulta de conectar dos proposiciones, p y q, mediante el conectivo .
Esta proposición compuesta de denota por y se lee p implica q.
En esta proposición compuesta, la proposición simple p se llama antecedente, mientras que la proposición simple q se llama consecuente.
La tabla de verdad para el conectivo está dada por
| p | q | |
|---|---|---|
| V | V | |
| V | F | |
| F | V | |
| F | F |
Se puede ver que una proposición compuesta tiene valor de verdad falso solamente cuando el antecedente es verdadero y el consecuente es falso. En cualquier otro caso, el valor de verdad de la proposición compuesta es verdadero.
Bicondicional
La bicondicional es la proposición compuesta que resulta de conectar dos proposiciones, p y q, mediante el conectivo .
Esta proposición compuesta se denota por y se lee p si y solo si q.
La tabla de verdad para el conectivo está dada por
| p | q | |
|---|---|---|
| V | V | |
| V | F | |
| F | V | |
| F | F |
Se puede ver que la proposición compuesta tiene valor de verdad verdadero siempre que las proposiciones simples tienen el mismo valor de verdad. Es cualquier otro caso, la proposición compuesta tiene valor de verdad falso
Propiedades de los Operadores Lógicos
Según el escritor (Carlos, 2005) se denominan también leyes, las leyes que se refieren a este conjunto de operadores vienen expresadas por pares, cada una de ellas es la ley Dual de la otra. Esta propiedad se expresa mediante el siguiente teorema de dualidad: sea x y y variables booleanas expresada con el conjunto de operadores. La expresión dual A es una expresión booleana obtenida de A por el intercambio de la conectividad.
Leyes de asociativa
x+ (y + z)=(x + y)= z x + y + z
x(y z)=(x y)=z= x y z
Leyes de idempotencia
x + x=x ; xx = x
Leyes de acotación
x+1= 1 ; x.0 = 0
Leyes de absorción
x + x y= x x(x +y)=x
Leyes de involución
(x´)´ = x ; (0´)´=0 (1´)´=1
Leyes de D´ Morgan
(x + y)´= x´. y´ ; (x. y´)´ ; x´+ y´
Formas Proposicionales
Se denominan formas proposicionales a las estructuras construidas por variables proposicionales y operadores lógicos.
Dada la estructura lógica de una forma proposicional se puede determinar si es tautología, de contingencia, o contradicción. (Intriago, 2015)
Tautología:
- Cuando se tienen proposiciones verdaderas para todos los valores de verdad de las variables proposicionales. (Intriago, 2015)
Ejemplos:
- Bésame con besos de tu boca
- Subir arriba
- Salir afuera
- Bajar abajo.
- Vive la vida
- Entrar adentro
Contradicción:
- Cuando se tienen proposiciones falsas para todos los valores de verdad de las variables proposicionales. (Intriago, 2015)
- Son cuando aquellas fórmulas que son falsas para cualquier valoración de símbolos proposicionales que contiene. Las proposiciones dan de resultado negativo. (Tautología, Contradicciones, Contingencias Lógicas - Lógica y su fundamento)
Ejemplos:
No es caro, cuesta mucho dinero.
La comida está salada, no tiene sal.
La torta es dulce, no es dulce.
Contingencia:
- Cuando se tienen proposiciones falsas y verdaderas para todos los valores de verdad de las variables proposicionales. (Intriago, 2015)
- Se refiere a algo que es probable que ocurra, aunque tenga la mayor seguridad al respecto. Por lo tanto, es lo posible o aquello que puede o no concretarse.
Ejemplos:
- Creo que me estoy enfermando.
- Dudo que el niño se duerma.
- Podrías leer este libro.
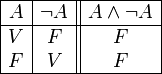
No hay comentarios:
Publicar un comentario