Geometría Analítica en el Plano

Puntos y Rectas

¿Qué es un punto?

El punto es el elemento base de la geometría, ente fundamental, porque con él determinamos las rectas y los planos. Podemos definirlo también, como la intercesión de dos líneas. Sirve para indicar una posición y no tiene dimensión.

¿Qué es una recta?

Una recta es una sucesión ininterrumpida de puntos con una misma dirección, por lo tanto sólo tiene una dimensión. Dos puntos determinan una recta la recta es infinita, no posee ni principio ni fin.

La recta tienen una dimensión, la longitud.

Tipos de rectas

• Recta: La recta propiamente dicha se caracteriza porque los puntos que la forman están en la misma dirección. Tiene una sola dirección y dos sentidos. No se puede medir.

• Semirrecta: Es línea recta que tiene origen pero no tiene fin, tiene sólo un sentido, y no se puede medir.

• Segmento: Un segmento es una línea recta que tiene principio y fin, un segmento se puede medir.

• Poligonal: Se llama recta poligonal aquella que está formada por varias porciones de rectas que están unas a continuación de otras, pero no están alineadas, la línea poligonal puede ser abierta (cuando ningún extremo se une) o cerrada (cuando el primer extremo se une con el último). La línea poligonal cerrada forma una figura plana que se llama polígono.

• Curva:Una curva está formada por puntos que están en distinta dirección. Puede ser curva abierta (los externos no se unen) curva cerrada (cuyos extremos se unen) y curva mixta (formada por lineas rectas y curvas unidas)

Posiciones de las rectas:

• Dos rectas son paralelas: si no tienen ningún punto en común.

• Dos rectas son secantes: cuando tienen un punto en común.

• Dos rectas son perpendiculares: cuando al cortarse forman cuatro ángulos rectos.

Posición de las rectas en el espacio

• Horizontal
• Vertical
• Inclinada

La linea curva puede ser:

• Circunferencia, es una curva regular cerrada, cuyos puntos están todos a la misma distancia de otro llamado centro.

• Elípse, es una curva regular cerrada que se diferencia de la anterior porque la suma de la distancia de cada uno de sus puntos respecto a otros dos que están en su interior es siempre igual.

• Espiral es una curva regular abierta que gira sobre sí misma.

• Parábola es una curva regular abierta, cada uno de sus puntos está a una distancia siempre igual de un punto fijo llamado foco y de una recta llamada directriz.

Ejercicios

Circunferencia

Una circunferencia (C) en negro, diámetro (D) en cian, radio (R) en rojo, y centro (O) en magenta

La circunferencia es una curva plana y cerrada donde todos sus puntos están a igual distancia del centro.

Una circunferencia es el lugar geométrico de los puntos de un plano que equidistan de otro punto fijo llamado centro.

Distíngase del círculo, que es el lugar geométrico de los puntos contenidos en el interior de dicha circunferencia, o sea, la circunferencia es el perímetro del círculo. Los puntos de la circunferencia están a una distancia igual al radio del centro del círculo, mientras los demás puntos del círculo están a menor distancia que el radio.

Puede ser considerada como una elipse de excentricidad nula, o una elipse cuyos semiejes son iguales, o los focos coinciden; o bien fuera una elipse cuyas directrices están en el infinito. También se puede describir como la sección, perpendicular al eje, de una superficie cónica o cilíndrica, o como un polígono regular de infinitos lados, cuya apotemacoincide con su radio.

La intersección de un plano con una superficie esférica puede ser: o bien el conjunto vacío (plano exterior); o bien un solo punto (plano tangente); o bien una circunferencia, si el plano secante pasa por el centro, se llama ecuador¹​

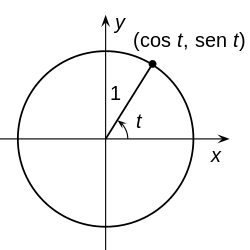
La circunferencia de centro en el origen de coordenadas y radio 1 se denomina circunferencia unidad o circunferencia goniométrica

Terminología de la circunferencia

Secantes, cuerdas y tangentes.

Existen varios puntos, rectas y segmentos, singulares en la circunferencia:

• Centro: Es el punto interior equidistante de todos los puntos de la circunferencia.
• Radio: Es el segmento que une el centro de la circunferencia con un punto cualquiera de la misma. El radio también es la longitud del segmento del mismo nombre. El radio es igual a la longitud de la circunferencia dividida entre 2π.
• Diámetro: El diámetro de una circunferencia es el segmento que une dos puntos de la circunferencia que pasa por el centro de esta. El diámetro también es la longitud del segmento del mismo nombre. El diámetro mide el doble del radio. El diámetro es igual a la longitud de la circunferencia dividida entre π.
• Cuerda: La cuerda es un segmento que une dos puntos de la circunferencia. El diámetro es la cuerda de longitud máxima.
• Recta secante: Es la línea que corta a la circunferencia en dos puntos.
• Recta tangente: Es la línea que toca a la circunferencia en un solo punto.
• Punto de Tangencia: es el punto de contacto de la recta tangente con la circunferencia.
• Arco: El arco de la circunferencia es cada una de las partes en que una cuerda divide a la circunferencia. Un arco de circunferencia se denota con el símbolo sobre las letras de los puntos extremos del arco.
• Semicircunferencia: cada uno de los dos arcos delimitados por los extremos de un diámetro.

Resultados analíticos

Longitud de la circunferencia

El interés por conocer la longitud de una circunferencia surge en Babilonia (actual Irak), cuando usaban los carros con rueda, era primordial relacionar el diámetro o radio con la circunferencia.⁷​ La longitud ${\displaystyle \ell }$ de una circunferencia es:

${\displaystyle \ell =2\pi r=\pi d}$

donde r es la longitud del radio y d=2r es el diámetro. Así pues ${\displaystyle \pi \,}$ (número pi) es, por definición, el cociente entre la longitud de la circunferencia y el diámetro:

${\displaystyle \pi ={\frac {\ell }{d}}={\frac {\ell }{2r}}}$

Área del círculo delimitado por una circunferencia

Área del círculo = π × área del cuadrado sombreado.

Arquímedes, en su tratado Sobre la medida del círculo, definió que el área del círculo era igual en área a un triángulo rectángulo, siendo uno de sus catetos la longitud ${\displaystyle \ell }$ de la circunferencia y el otro el radio r. Así, el área del círculo delimitado por la circunferencia es:

${\displaystyle {\text{Área}}={\frac {1}{2}}\ell r=\pi r^{2}}$

Ecuaciones de la circunferencia

Ecuación en coordenadas cartesianas

circunferencia de radio dos en un sistema de coordenadas

En un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el punto (a, b) y radio r consta de todos los puntos (x, y) que satisfacen la ecuación

${\displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}\,}$.

Cuando el centro está en el origen (0, 0), la ecuación anterior se simplifica a

${\displaystyle x^{2}+y^{2}=r^{2}\,}$.

La circunferencia con centro en el origen y de radio la unidad, es llamada circunferencia goniométrica, circunferencia unidad o circunferencia unitaria.

De la ecuación general de una circunferencia se deduce que:

${\displaystyle x^{2}+y^{2}+Dx+Ey+F=0\,}$

resultando:

${\displaystyle a=-{\frac {D}{2}}}$

${\displaystyle b=-{\frac {E}{2}}}$

${\displaystyle r={\sqrt {a^{2}+b^{2}-F}}}$

Si conocemos los puntos extremos de un diámetro: ${\displaystyle (x_{1},y_{1}),(x_{2},y_{2})\,}$, la ecuación de la circunferencia es:

${\displaystyle (x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})=0.\,}$

Ecuación vectorial de la circunferencia

En el espacio vectorial R², la circunferencia con centro en el origen y radio R, viene dada por la ecuación vectorial:

${\displaystyle \mathbf {r} (\theta )=(R\cos(\theta ),R\operatorname {sen}(\theta ))\,}$,

donde ${\displaystyle \theta \,}$ es el parámetro de la curva, además cabe destacar que ${\displaystyle \theta \in [0,2\pi )}$. Se puede deducir fácilmente desde la ecuación cartesiana, ya que la componente x y la componente y, al cuadrado y sumadas deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio vectorial R³ esta misma ecuación da como resultado un cilindro, dejando el parámetro z libre.

De manera más general, si c es un punto fijo, x un punto variable cualquiera (ambos de R²) y r un real positivo, la ecuación vectorial

${\displaystyle \|\mathbf {x} -\mathbf {c} \|=r}$

representa una circunferencia de centro c y radio r.⁸​ La doble barra vertical representa la norma vectorial; en este caso corresponde a la distancia euclidianaconstante de valor r.

Ecuación en coordenadas polares

Circunferencia unitaria.

Cuando la circunferencia tiene centro en el origen y el radio es c, se describe en coordenadas polares como ${\displaystyle (r,\theta )\,}$

${\displaystyle r=c.\,}$

Cuando el centro no está en el origen, sino en el punto ${\displaystyle (s,\alpha )\,}$ y el radio es ${\displaystyle c\,}$, la ecuación se transforma en:

${\displaystyle r^{2}-2sr\cos(\theta -\alpha )+s^{2}=c^{2}}$

Ecuación paramétrica de la circunferencia

La circunferencia con centro en (a, b) y radio r se parametriza con funciones trigonométricas como:

${\displaystyle {\begin{cases}x=&a+r\cos t\\y=&b+r\,\operatorname {sen} t\end{cases}}\qquad t\in [0,2\pi )}$

donde t es el parámetro, que varía en el rango indicado. También se puede parametrizar con funciones funciones racionales como

${\displaystyle {\begin{cases}x=&a+r\left({\frac {1-t^{2}}{1+t^{2}}}\right)\\y=&b+r\left({\frac {2t}{1+t^{2}}}\right)\end{cases}}\qquad t\in {\widehat {\mathbb {R} }}}$

donde t no solo recorre todos los valores reales, sino también un punto en el infinito.⁹​

Ecuación en el plano complejo

En el plano complejo, una circunferencia con centro c y radio (r) tiene como ecuación ${\displaystyle |z-c|=r\,}$. En forma paramétrica puede ser escrita como ${\displaystyle z=re^{it}+c}$.

Propiedades geométricas

La circunferencia y un punto

Un punto en el plano puede ser:

• Exterior a la circunferencia, si la distancia del centro al punto es mayor que la longitud del radio.
• Perteneciente a la circunferencia, si la distancia del centro al punto es igual a la longitud del radio.
• Interior a la circunferencia, si la distancia del centro al punto es menor a la longitud del radio. El conjunto de todos los puntos interiores se llama interior de la circunferencia. Respecto al círculo, claramente, se distinguen el interior, el exterior y la frontera, que es precisamente la respectiva circunferencia.¹⁰​

La circunferencia y la recta

Una recta, respecto de una circunferencia, puede ser:

• Exterior, si no tienen ningún punto en común con ella y la distancia del centro a la recta es mayor que la longitud del radio.

• Tangente, si la toca en un punto (el punto de tangencia o tangente) y la distancia del centro a la recta es igual a la longitud del radio. Una recta tangente a una circunferencia es perpendicular al radio que une el punto de tangencia con el centro.

• Secante, si tiene dos puntos comunes, es decir, si la corta en dos puntos distintos y la distancia del centro a la recta es menor a la longitud del radio.

• Segmento circular, es el conjunto de puntos de la región circular comprendida entre una cuerda y el arco correspondiente

Dos circunferencias

Dos circunferencias, en función de sus posiciones relativas, se denominan:

• Exteriores o Disjuntas, si no tienen puntos comunes y la distancia que hay entre sus centros es mayor que la suma de sus radios. No importa que tengan igual o distinto radio. (Figura 1)

• Tangentes exteriormente, si tienen un punto común y todos los demás puntos de una son exteriores a la otra. La distancia que hay entre sus centros es igual a la suma de sus radios. No importa que tengan igual o distinto radio. (Figura 2)

• Secantes, si se cortan en dos puntos distintos y la distancia entre sus centros es menor a la suma de sus radios. No importa que tengan igual o distinto radio. Dos circunferencias distintas no pueden cortarse en más de dos puntos. Dos circunferencias son secantes ortogonalmente si el ángulo entre sus tangentes en los dos puntos de contacto es recto. (Figura 3)

• Tangentes interiormente, si tienen un punto común y todos los demás puntos de una de ellas son interiores a la otra exclusivamente. La distancia que hay entre sus centros es igual al valor absoluto de la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra. (Figura 4)

• Interiores excéntricas, si no tienen ningún punto común y la distancia entre sus centros es mayor que 0 y menor que el valor absoluto de la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra.

• Interiores concéntricas, si tienen el mismo centro (la distancia entre sus centros es 0) y distinto radio. Forman una figura conocida como corona circular o anillo. Una de ellas tiene que tener mayor radio que la otra. (Figura 5)

• Coincidentes, si tienen el mismo centro y el mismo radio. Si dos circunferencias tienen más de dos puntos comunes, necesariamente son circunferencias coincidentes.

Ángulos en una circunferencia

Ángulos en la circunferencia.

Arco capaz: los cuatro ángulos inscritos determinan el mismo arco y por tanto son iguales.

Un ángulo, respecto de una circunferencia, pueden ser:

Ángulo central, si tiene su vértice en el centro de esta. Sus lados contienen a dos radios.

La amplitud de un ángulo central es igual a la del arco que abarca.

Ángulo inscrito, si su vértice es un punto de la circunferencia y sus lados contienen dos cuerdas.

La amplitud de un ángulo inscrito en una semi circunferencia equivale a la mayor parte del ángulo exterior que limita dicha base. (Véase: arco capaz.)

Ángulo semi-inscrito, si su vértice es un punto de la circunferencia y sus lados contienen una cuerda y una recta tangente a la circunferencia. El vértice es el punto de tangencia.

La amplitud de un ángulo semi-inscrito es la mitad de la del arco que abarca.

Ángulo interior, si su vértice está en el interior de la circunferencia.

La amplitud de un ángulo interior es la mitad de la suma de dos medidas: la del arco que abarcan sus lados más la del arco que abarcan sus prolongaciones.

Ángulo exterior, si tiene su vértice en el exterior de la circunferencia.

Ejercicios

PARÁBOLA

• 
  

Una parábola es el lugar geométrico de los puntos que equidistan de un punto fijo, llamado foco y de una recta fija llamada directriz.

La parábola es una sección cónica, resultado de la intersección de un conorecto con un plano que corta a la base del mismo, oblicuo a su eje y paralelo a una directriz g.

El foco y la directriz determinan cómo va a ser la apariencia de la parábola (en el sentido de que será más o menos abierta según sea la distancia entre F y la directriz).

Una de las aplicaciones físicas más importantes de la parábola es el movimiento parabólico. Este movimiento se caracteriza porque una partícula o cuerpo sólido lanzado en un campo gravitatorio recorre una trayectoria parabólica.

Una aplicación práctica de la parábola son las antenas parabólicas, en las que todas las rectas paralelas al eje de la parábola se reflejan en el foco de la misma. (Empleado en óptica, antenas de transmisión de radiofrecuencia, estufas domésticas parabólicas, captación de energía solar, etc.)

Elementos de una parábola

Los elementos de la parábola son:

• Foco: el foco F es el punto fijo. Los puntos de la parábola equidistan del foco y la directriz.
• Directriz: es la recta fija D. Los puntos de la parábola equidistan de la directriz y el foco.
• Radio vector: es el segmento R que une el foco con cada uno de los puntos de la parábola.
• Eje: es la recta E perpendicular a la directriz que pasa por el foco.

• Parámetro: es el vector p, que va desde el foco al punto más próximo de la directriz
• Vértices: es el punto V de la intersección del eje y la parábola.
• Puntos interiores y exteriores: la parábola divide el plano en dos regiones. Los puntos que están en la región del foco se llaman puntos interiores (I), mientras que los otros son los exteriores (J).

Ecuación de la parábola

La ecuación de la parábola depende de si el eje es vertical u horizontal. Si el eje es vertical, la y será la variable dependiente. Si el eje es horizontal, será x la variable dependiente.

Eje vertical

La ecuación de la parábola a partir del vértice siendo el eje vertical es:

La ecuación general de la parábola con el eje vertical es la siguiente:

El parámetro a indica lo “abierta” que es la parábola. Si el parámetro a es positivo, el vértice será el mínimo de la parábola. Si a es negativo, será el máximo.

Eje horizontal

La ecuación de la parábola a partir del vértice siendo el eje horizontal es:

La ecuación general de la parábola con el eje horizontal es la siguiente:

El parámetro a indica lo “abierta” que es la parábola.

Ecuación general de la parábola

Los casos anteriores donde el eje es vertical u horizontal, son casos particulares de la ecuación general de la parábola.

Ejercicios

ELIPSE

La elipse es el lugar geométrico de los puntos del plano cuya suma de las distancias a los dos focos (puntos interiores fijos F₁ y F₂) es constante. Es decir, para todo punto a de la elipse, la suma de las distancias d₁ y d₂ es constante.

También podemos definir la elipse como una cónica, consecuencia de la intersección de un cono con un plano oblicuo que no corta la base.

Elementos de una elipse

Los elementos más importante de la elipse son:

• Focos: son los puntos fijos F₁ y F₂ que generan la elipse. La suma de las dos distancias de cualquier punto de la elipse a los dos focos (d₁ y d₂) es constante.
• Distancia focal (2c): distancia entre los dos focos. F₁F₂=2c. c es la semidistancia focal.
• Centro: es el punto medio de los dos focos (O).
• Semieje mayor: longitud del segmento OI o OK (a). La longitud es mayor (o igual en el caso de la circunferencia) a la del semieje menor. La suma de las distancias de cualquier punto de la elipse a los focos es constante y ésta es igual a dos veces el semieje mayor:
  
  
  

• Semieje menor: longitud del segmento OJ o OL (b). Ambos semiejes son los dos ejes de simetría de la elipse. Se cumple que:
  
  
  
  Como vemos en el dibujo, esta relación cumple el teorema de Pitágoras.
• Radios vectores: los radios vectores de cualquier punto de la elipse (P=(x,y)) son los dos segmentos que lo unen con los dos focos. PF₁ y PF₂ (en el dibujo, d₁ y d₂).
• Vértices: son los puntos resultantes de la intersección de la elipse con la recta que pasa por los focos, F₁F₂, y su perpendicular que pasa por el centro. Es decir, son los puntos I, J, K y L

Ecuación de una elipse

Los puntos pertenecientes a la elipse (x,y) son los puntos del plano que cumplen que la suma de su distancia a los dos focos es constante. La ecuación de la elipse es la siguiente:

En el caso de que la elipse esté centrada (el centro es el punto (0,0)), la ecuación es:

Área de una elipse

El área comprendida dentro de una elipse es π veces el producto de los dos semiejes (a y b).

En el caso de que los dos semiejes sean iguales (r=a=b), su fórmula es la misma que el área comprendida dentro de una circunferencia (o lo que es lo mismo, el área del círculo):

Perímetro de una elipse

El cálculo del perímetro de la elipse (o longitud de la elipse) es muy difícil, aunque no lo parezca. Requiere de integrales complicadas para su cálculo. Existen fórmulas que aproximan el cálculo hasta valores bastante exactos. Existe una aproximación con menos del 5% de error, siempre que el semieje mayor (a) no sea mucho más grande que el menor (b):

El matemático Ramanujan dio una aproximación más exacta que la anterior :

Excentricidad de la elipse

La excentricidad de una elipse (e) es un valor que determina la forma de la elipse, en el sentido de si es más redondeada o si se aproxima a un segmento. Sea c la semidistancia focal y a el semieje mayor:

La excentricidad puede tomar valores entre 0 y 1 (0≤e≤1). Es 0 cuando la elipse es una circunferencia. En este caso los semiejes mayor y menor son iguales y los focos (F₁ y F₁) coinciden en el centro de la elipse. Cuando la excentricidad crece y tiende a 1, la elipse se aproxima a un segmento.

Existe otra fórmula que calcula la excentricidad a partir de los dos semiejes (a y b).

Esta fórmula se obtiene a partir de la anterior ya que se cumple que:

Ejercicios