Geometría Plana

Figuras Geométricas en el Plano 

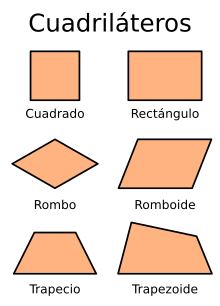
Cuadriláteros

Son polígonos que tienen cuatro lados.

Paralelogramos: Son cuadriláteros que tienen sus lados paralelos dos a dos. Son paralelogramos el rectángulo, el cuadrado y el rombo.

El área de los paralelogramos es el producto de la base por la altura.

Trapecio: es un cuadrilátero que tiene dos lados paralelos.

El área del trapecio A = 1/2(a + b)h

Pentágono

Es un polígono que tiene 5 lados (el número de lados siempre es igual al de ángulos). Si todos los lados y todos los ángulos son iguales se llama pentágono regular.

Para calcular el área y el perímetro de un pentágono regular ver el apartado ‘polígono regular de n lados’.

Hexágono

Es un polígono que tiene 6 lados (el número de lados siempre es igual al de ángulos). Si todos los lados y todos los ángulos son iguales se llama hexágono regular.

Para calcular el área y el perímetro de un hexágono regular ver el apartado ‘polígono regular de n lados’

.

Heptágono

Es un polígono que tiene 7 lados (el número de lados siempre es igual al de ángulos). Si todos los lados y todos los ángulos son iguales se llama heptágono regular.

Para calcular el área y el perímetro de un hexágono regular ver el apartado ‘polígono regular de n lados’.

Octagono

Es un polígono que tiene 8 lados (el número de lados siempre es igual al de ángulos). Si todos los lados y todos los ángulos son iguales se llama octógono regular.

Para calcular el área y el perímetro de un octógono regular ver el apartado ‘polígono regular de n lados’.

Nonágono

Es un polígono que tiene 9 lados (el número de lados siempre es igual al de ángulos). Si todos los lados y todos los ángulos son iguales se llama nonágono regular.

Para calcular el área y el perímetro de un nonágono regular ver el apartado ‘polígono regular de n lados’.

Decágono

Es un polígono que tiene 10 lados (el número de lados siempre es igual al de ángulos). Si todos los lados y todos los ángulos son iguales se llama decágono regular.

Para calcular el área y el perímetro de un pentágono regular ver el apartado ‘polígono regular de n lados’.

Clases de Rectas en el Plano

Secantes

Las rectas secantes se cortan en un punto.

Paralelas

Las rectas paralelas no se cortan en ningún punto.

Coincidentes

Dos rectas son coincidentes si todos sus puntos son comunes.

Perpendiculares

Dos rectas son perpendiculares cuando al cortarse forman cuatro ángulos iguales de 90º.

Coincidentes

Dos rectas son coincidentes si todos sus puntos son comunes

Ángulos

Se toma un punto del plano y partiendo de ese punto, se dibujan dos semirrectas. A la abertura formada por las dos semirrectas se le llama ángulo.

Definición de ángulo

Se llama ángulo a la parte del plano delimitada por dos semirrectas que parten de un mismo punto llamado vértice. A cada semirrecta se le llama lado del ángulo.

- Los lados del ángulo son las semirrectas que lo forman.

- El vértice del ángulo es el punto común que es origen de los lados.

Los tipos de ángulos son:

Agudo < 90°

Recto = 90°

Obtuso > 90°

Convexo < 180°

Llano = 180°

Cóncavo > 180°

Completo = 360°

Nulo = 0º

Hoy hablaremos de los ángulos agudo, recto y obtuso.

 Tipos de ángulos según su medida

Agudo < 90°	Recto = 90°	Obtuso>90°

 

 Ángulos rectos

Un ángulo recto es un ángulo que mide exactamente 90°. Si te das cuenta, en la esquina del ángulo hay un símbolo especial, una caja. Si ves ese símbolo, el ángulo es recto. No se suele escribir el 90°. Si ves la caja en la esquina ya te están diciendo que es un ángulo recto.

Un ángulo recto puede estar en cualquier orientación o giro, lo que importa es que el ángulo interior sea 90°

 Ángulos agudos

Un ángulo agudo es un ángulo que mide menos de 90°. 

Acuérdate de fijarte en cuál de los dos ángulos es al que se refiere uno. Si el ángulo pequeño es menor que 90°, entonces ese es agudo.

Ángulos obtusos

Un ángulo obtuso es un ángulo que mide más de 90° pero menos de 180°. 

 

Acuérdate de fijarte en cuál de las dos partes es a la que se refiere uno. El ángulo más pequeño entre laslíneas es obtuso si mide entre 90° y 180°.

 Algunas cosas importantes que debes saber

Los ángulos que miden 180° se denominan ángulos extendidos o llanos.

Los ángulos que miden más de 180° y menos de 360° se denominan ángulos cóncavos.

Los ángulos que miden 360° se denominan ángulos completos.

El ángulo nulo está formado por dos semirrectas coincidentes, por lo que su abertura es nula, es decir, 0°.

Los ángulos pueden nombrarse utilizando letras griegas. Por ejemplo:

 

 

Poligonales y Polígonos

Las líneas poligonales son varios segmentos de rectas unidos.

Las líneas poligonales se pueden clasificar en abiertas y cerradas.

• Una línea poligonal es abierta cuando los extremos no coinciden en el mismo punto. Es decir, si trazamos la línea empezando por uno extremo terminamos de dibujarla terminando en otro punto diferente.
  Esto es un ejemplo de línea poligonal abierta:
• Una línea poligonal es cerrada cuando los extremos sí coinciden en el mismo punto. Es decir, empezando a dibujar la línea en un punto, podemos terminar de trazarla terminando en el mismo punto.
  Esto es un ejemplo de línea poligonal cerrada:

LÍNEAS POLIGONALES Y POLÍGONOS.

Línea poligonal: una línea poligonal está formada por varios segmentos consecutivos.

Las líneas poligonales pueden ser abiertas o cerradas.

Polígono: es la región de plano limitada por una línea poligonal cerrada.

ELEMENTOS DE UN POLÍGONO

Lado: es cada uno de los segmentos que forman la línea poligonal que limita al

polígono.

Vértice: son los puntos donde se cortan los lados.

Ángulo: la región de plano comprendida entre dos lados al cortarse en un punto

llamado vértice.

Diagonal: son los segmentos que unen dos vértices no consecutivos.

Cualquier polígono tiene el mismo número de lados, de ángulos y de vértices.

Perímetro: perímetro de un polígono es la suma de las longitudes de sus lados. O lo que

es lo mismo, la medida de la línea poligonal cerrada que lo comprende.

CLASES DE POLÍGONOS.

Los polígonos se clasifican por su número de lados en:

Los polígonos que tienen todos sus lados y ángulos iguales se llaman polígonos regulares.

En caso contrario los polígonos son irregulares.

CLASIFICACIÓN DE LOS TRIÁNGULOS.

Los triángulos son los polígonos de 3 lados. Por tanto tienen 3 ángulos y tres vértices.

Según sus lados los triángulos se clasifican en:

Equilátero:tiene los tres lados iguales

Isósceles: tiene dos lados iguales

Escaleno: tiene los tres lados distintos

Según sus ángulos los triángulos se clasifican en:

CLASIFICACIÓN DE LOS CUADRILÁTEROS.

Los cuadriláteros son polígonos de cuatro lados y cuatro ángulos.

Los cuadriláteros se clasifican en paralelogramos, trapecios y trapezoides.

-Los paralelogramos son los cuadriláteros que tienen sus lados paralelos dos a dos.

Existen cuatro tipos de paralelogramos:

Cuadrado: Cuatro lados y cuatro ángulos iguales.

Rombo: Cuatro lados iguales y los ángulos iguales dos a dos.

Rectángulo: Lados iguales dos a dos y los cuatro ángulos iguales.

Romboide: Lados y ángulos iguales dos a dos.

- Los trapecios sólo tienen dos lados paralelos, Tres tipos de trapecios:

Trapecio rectángulo: Dos ángulos rectos.

Trapecio isósceles: Lados no paralelos iguales y ángulos iguales dos a dos.

Trapecio escaleno: Cuatro lados y cuatro ángulos desiguales.

-Los trapezoides no tienen ningún lado paralelo.

Triángulo

El triángulo es un polígono de tres lados y tres ángulos.

Un triángulo en geometría plana, es un polígono de tres segmentos que determinan tres puntos del plano no colineales. Los puntos comunes a cada par de segmentos se denominan vértices del triángulo¹​ y los segmentos son los lados del triángulo.

Un triángulo tiene tres ángulos interiores, tres pares congruentes de ángulos exteriores,²​ tres lados y tres vértices entre otros elementos.

Si está contenido en una superficie plana se denomina triángulo, o trígono, un nombre menos común para este tipo de polígonos. Si está contenido en una superficie esférica se denomina triángulo esférico. Representado, en cartografía, sobre la superficie terrestre, se llama triángulo geodésico.

Elementos

Triángulo: ${\displaystyle ABC}$ de lados ${\displaystyle a,b,c}$ y de ángulos interiores ${\displaystyle \alpha ,\beta ,\gamma .}$

Vértices[editar]

Cada uno de los puntos que determinan un triángulo. Tal como los vértices de un polígono, suelen ser denotados por letras latinas mayúsculas: ${\displaystyle A,B,C,...}$. Si ${\displaystyle AB+BC=AC}$ no existe triángulo que determine ${\displaystyle A,B}$ y ${\displaystyle C}$.

Un triángulo se nombra entonces como cualquier otro polígono, designando sucesivamente sus vértices, por ejemplo ABC. En el caso del triángulo, los vértices pueden darse en cualquier orden, porque cualquiera de las 6 maneras posibles (ABC, ACB, BAC, BCA, CAB, CBA), corresponde a un recorrido de su perímetro. Esto ya no es cierto para polígonos con más vértices.

Lados[editar]

Cada par de vértices determina un segmento, que se conoce como lado del triángulo. No interesa el orden de los vértices para nombrar un lado de modo AB, BA nombran a un mismo lado.

Los lados del triángulo se denotan, como todos los segmentos, por sus extremos: AB, BC y AC.

Para nombrar la longitud de un lado, por lo general se utiliza el nombre del vértice opuesto, convertido a minúscula latina: ${\displaystyle a}$ para BC, ${\displaystyle b}$ para AC, ${\displaystyle c}$ para AB.

La suma de los lados de un triángulo se conoce como perímetro, denotado por p o 2s; cumple la ecuación ${\displaystyle p=2s=AB+BC+CA}$

Ángulos[editar]

Cada par de lados con origen común el vértice de un triángulo y que contienen dos de esos lados concurrentes se llama ángulo del triángulo u -ocasionalmente- ángulo interior-

La notación general para el ángulo entre dos segmentos OP y OQ prolongados y que concurren en el extremo O es ${\displaystyle {\widehat {POQ}}.\,}$

También es posible utilizar una letra minúscula -habitualmente una letra griega- coronada por un acento circunflejo (en rigor, los ángulos deben ser designados por letras mayúsculas y su medida por minúsculas, pero a menudo se utilizan los mismos nombres para los dos con el fin de simplificar la notación). En el caso de un triángulo, el ángulo entre dos lados todavía puede, por tolerancia y en ausencia de ambigüedad, ser designado por el nombre del vértice común, coronado por un acento circunflejo. En resumen, en el ejemplo se pueden observar los ángulos:

${\displaystyle {\widehat {\alpha }}={\widehat {a}}={\widehat {A}}={\widehat {BAC}},\ {\widehat {\beta }}={\widehat {b}}={\widehat {B}}={\widehat {ABC}},\ {\widehat {\gamma }}={\widehat {c}}={\widehat {C}}={\widehat {ACB}}.\,}$

EL ángulo cuyo vértice coincide con uno de los vértices del triángulo y sus lados: son la prolongación de un lado triangular y el otro lado angular contiene a un lado triangular, se llama ángulo externo. En cada vértice triangular hay dos ángulos externos.³​

Triángulos — Resumen de convenciones de designación

Vértices	${\displaystyle {\text{A}}}$	${\displaystyle {\text{B}}}$	${\displaystyle {\text{C}}}$
Lados (como segmento)	${\displaystyle {\text{BC}}}$	${\displaystyle {\text{AC}}}$	${\displaystyle {\text{AB}}}$
Lados (como longitud)	${\displaystyle a}$	${\displaystyle b}$	${\displaystyle c}$
Ángulos	${\displaystyle {\widehat {\alpha }}={\widehat {a}}={\widehat {A}}={\widehat {BAC}}}$	${\displaystyle {\widehat {\beta }}={\widehat {b}}={\widehat {B}}={\widehat {ABC}}}$	${\displaystyle {\widehat {\gamma }}={\widehat {c}}={\widehat {C}}={\widehat {ACB}}}$

Clasificación de los triángulos[editar]

Los triángulos se pueden clasificar por la relación entre las longitudes de sus lados o por la amplitud de sus ángulos.

Por las longitudes de sus lados[editar]

Por las longitudes de sus lados, todo triángulo se clasifica:

• Como triángulo equilátero, cuando los tres lados del triángulo tienen una misma longitud (los tres ángulos internos miden 60 grados o ${\displaystyle \pi /3\,}$ radianes).

• Como triángulo isósceles (del griego ἴσος "igual" y σκέλη "piernas", es decir, "con dos piernas iguales"), si tiene dos lados de la misma longitud. Los ángulos que se oponen a estos lados tienen la misma medida. (Tales de Mileto, filósofo griego, demostró que un triángulo isósceles tiene dos ángulos iguales, estableciendo así una relación entre longitudes y ángulos; a lados iguales, ángulos iguales⁴​).

Un triángulo es isósceles cuando tiene dos lados iguales; esto no descarta que los tres lados sean iguales, de modo que todo triángulo equilátero sea isósceles, pero no se cumple el enunciado recíproco.⁵​

Sea el triángulo ABC isósceles, donde b = c entonces los ángulos opuestos son iguales, i.e B = C. También se cumple que B' = C' siendo estos los ángulos externos.Además se cumplen las igualdades

A + 2B = A +2C = 180º;

A^' + 2B^' = A^' + 2C^' = 360º; A^' = 2C = 2B; B^'=C^'=A+B= A+C

${\displaystyle m_{a}=h_{a}=v_{A}={\frac {1}{2}}{\sqrt {4b^{2}-a^{2}}}}$ donde ${\displaystyle m_{a},h_{a},v_{A}}$ son la mediana, altura del lado a y bisectriz de su ángulo A opuesto.⁶​

• Como triángulo escaleno (del griego σκαληνός "desigual"), si todos sus lados tienen longitudes diferentes (en un triángulo escaleno no hay dos ángulos que tengan la misma medida).

Equilátero	Isósceles	Escaleno

Por la amplitud de sus ángulos[editar]

Por la amplitud de sus ángulos los triángulos se clasifican en:

(Clasificación por amplitud de sus ángulos) Triángulos Rectángulos Oblicuángulos Obtusángulos Acutángulos

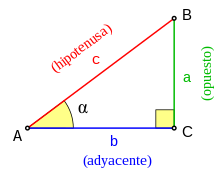
• Triángulo rectángulo: si tiene un ángulo interior recto (90°). A los dos lados que conforman el ángulo recto se les denomina catetos y al otro lado hipotenusa.
• Triángulo oblicuángulo: cuando ninguno de sus ángulos interiores es recto (90°). Por ello, los triángulos obtusángulos y acutángulos son oblicuángulos.Cualquier triángulo o bien es rectángulo o bien oblicuángulo. ⁷​
• Triángulo obtusángulo: si uno de sus ángulos interiores es obtuso (mayor de 90°); los otros dos son agudos (menores de 90°).
• Triángulo acutángulo: cuando sus tres ángulos interiores son menores de 90°.

Rectángulo	Obtusángulo	Acutángulo
	${\displaystyle \underbrace {\qquad \qquad \qquad \qquad \qquad \qquad } _{}}$
	Oblicuángulos

Clasificación según los lados y los ángulos del triángulo[editar]

Los triángulos acutángulos pueden ser:

• Triángulo acutángulo isósceles: con todos los ángulos agudos, siendo dos iguales, y el otro distinto. Este triángulo es simétrico respecto de su altura sobre el lado distinto.
• Triángulo acutángulo escaleno: con todos sus ángulos agudos y todos diferentes, no tiene eje de simetría.
• Triángulo acutángulo equilátero: sus tres lados y sus tres ángulos son iguales. Las tres alturas son ejes de simetría (dividen al triángulo en dos triángulos iguales).

Los triángulos rectángulos pueden ser:

• Triángulo rectángulo isósceles: con un ángulo recto y dos agudos iguales (de 45° cada uno), dos lados son iguales y el otro diferente: los lados iguales son los catetos y el diferente es la hipotenusa. Es simétrico respecto a la altura de la hipotenusa, que pasa por el ángulo recto.
• Triángulo rectángulo escaleno: tiene un ángulo recto, y todos sus lados y ángulos son diferentes.

Los triángulos obtusángulos pueden ser:

• Triángulo obtusángulo isósceles: tiene un ángulo obtuso, y dos lados iguales que son los que forman el ángulo obtuso; el otro lado es mayor que estos dos.
• Triángulo obtusángulo escaleno: tiene un ángulo obtuso y todos sus lados son diferentes.

Triángulo	equilátero	isósceles	escaleno
acutángulo
rectángulo
obtusángulo

Clasificación según la calidad de un triángulo[editar]

La medida de la calidad de triángulo (abreviada como CT) se determina por el producto de tres factores que se obtienen de la suma de dos de sus lados menos el tercero en forma cíclica, dividido por el producto de sus tres lados; y se representa mediante la siguiente fórmula:

${\displaystyle CT={\frac {(a+b-c)(b+c-a)(c+a-b)}{abc}}}$

donde a, b, c son las longitudes de los lados del triángulo.

Por lo tanto, si

• CT = 1 es un triángulo equilátero.
• CT = 0 es un triángulo degenerado.
• CT > 0.5 es un triángulo de calidad buena.

En otras palabras, la calidad del triángulo se aproxima a cero cuando la distancia euclidiana de uno de sus lados es cercana a cero o cuando los tres puntos del triángulo tienden a ser colineales.

La calidad de los triángulos tiene muchas aplicaciones en los métodos de triangulación como es el caso de la Triangulación de Delaunay porque se necesitan generar una serie de puntos en el espacio para que la malla que se genere sea de buena calidad debido a la cantidad de punto que se encuentran bien distribuidos en un espacio de dos dimensiones porque cuando se le asigne un valor o magnitud a cada punto de la malla la aproximación del triángulo va a tener un error mayor y la solución seria continuar asignando punto en el espacio de dos dimensiones para que la aproximación ser mejor y el error disminuya.

Congruencia de triángulos[editar]

Artículo principal: Congruencia de triángulos

Dos triángulos son congruentes si hay una correspondencia entre sus vértices de tal manera que el ángulo del vértice y los lados que lo componen, en uno de los triángulos, sean congruentes con los del otro triángulo.

Postulados de congruencia[editar]

Triángulo	Postulados de congruencia
	Postulado LAL (Lado, Ángulo, Lado) Dos triángulos son congruentes si dos lados de uno tienen la misma longitud que dos lados del otro triángulo, y los ángulos comprendidos entre esos lados tienen también la misma medida.
	Postulado ALA (Ángulo, Lado, Ángulo) Dos triángulos son congruentes si dos ángulos interiores y el lado comprendido entre ellos tienen la misma medida y longitud, respectivamente. (El lado comprendido entre dos ángulos es el lado común a ellos).
	Postulado LLL (Lado, Lado, Lado) Dos triángulos son congruentes si cada lado de un triángulo tiene la misma longitud que los correspondientes del otro triángulo.

Teoremas de congruencia[editar]

Triángulo	Teoremas de congruencia
	Teorema AAL (Ángulo, Ángulo, Lado) Dos triángulos son congruentes si dos ángulos y un lado, no comprendido entre los ángulos, tienen la misma medida y longitud, respectivamente.

Congruencia de triángulos rectángulos[editar]

• Criterio HC (Hipotenusa, Cateto). Dos triángulos rectángulos son congruentes si la hipotenusa y el cateto de uno de los triángulos tienen la misma medida que los correspondientes del otro.
• Criterio CC (Cateto, Cateto). Dos triángulos rectángulos son congruentes si los catetos de uno de los triángulos tienen la misma medida que los catetos correspondientes del otro.
• Criterio HA (Hipotenusa, Ángulo). Dos triángulos rectángulos son congruentes si la hipotenusa y un ángulo agudo de uno de los triángulos tienen la misma medida que los correspondientes del otro.
• Criterio CA (Cateto, Ángulo). Dos triángulos rectángulos son congruentes si el cateto y un ángulo agudo (el adyacente o el opuesto) de uno de los triángulos tienen la misma medida que los correspondientes del otro.

Semejanza de triángulos[editar]

Artículo principal: Triángulos semejantes

• Criterio AA (Ángulo, Ángulo). Si dos de sus ángulos son semejantes.
• Criterio LAL (Lado, Ángulo, Lado). Si dos de sus lados son proporcionales y el ángulo comprendido entre ellos es congruente.
• Criterio LLL (Lado, Lado, Lado). Si sus tres lados son proporcionales.

Semejanza de triángulos rectángulos[editar]

Dos triángulos rectángulos son semejantes si cumplen con al menos uno de los criterios siguientes:

• Si uno tiene un ángulo agudo de igual amplitud que un ángulo agudo del otro.
• Si uno tiene los dos catetos proporcionales con los del otro.
• Si uno tiene un cateto y la hipotenusa proporcionales con los del otro.

Corona triangular[editar]

Se consideran dos triángulos semejantes con lados paralelos y con circuncentro común ( centro de la circunferencia circunscrita). La intersección del exterior del triángulo de menor área con el interior del triángulo de mayor área unida con los dos triángulos forma una región en el plano que se llama corona triangular.⁸​

La frontera de esta región es la unión de los dos triángulos. Un punto es interior si está entre las intersecciones que determina un rayo con origen en el circuncentro con los lados homólogos. El conjunto de los puntos interiores es el interior de la región. Un punto está en el exterior de la región si no está en la frontera ni en el interior. El interior es convexo, abierto y conexo. La frontera es la unión disjunta de dos poligonales cerradas. El exterior es un conjunto desconexo, abierto y no convexo. La corona triangular es un conjunto cerrado, conexo y convexo.⁹​ La corona triangular es homeomorfa con la corona circular, tienen las mismas propiedades topológicas.

Propiedades de los triángulos[editar]

Un cuadrilátero con sus diagonales.

Un tetraedro.

Un triángulo puede ser definido como un polígono de tres lados, o como un polígono con tres vértices. El triángulo es el polígono más simple y el único que no tiene diagonal. Tres puntos no alineados definen siempre un triángulo (tanto en el plano como en el espacio).

Si se agrega un cuarto punto coplanar y no alineado, se obtiene un cuadrilátero que puede ser dividido en triángulos como el de la figura de la izquierda. En cambio, si el cuarto punto agregado es no coplanary no alineado, se obtiene un tetraedro que es el poliedro más simple y está conformado por 4 caras triángulares.

Todo polígono puede ser dividido en un número finito de triángulos, esto se logra por triangulación. El número mínimo de triángulos necesarios para esta división es n-2, donde n es el número de lados del polígono. El estudio de los triángulos es fundamental para el estudio de otros polígonos, por ejemplo para la demostración del Teorema de Pick.

En geometría euclidiana¹⁰​ la suma de los tres ángulos internos de un triángulo es siempre 180°, lo que equivale a π radianes:

${\displaystyle \alpha +\beta +\gamma =180{}^{\circ }=\pi }$

La suma de los ángulos de un triángulo es 180 grados.

Euclides había demostrado este resultado en sus Elementos (proposición I-32) de la siguiente manera: se traza una paralela a la línea (AB) que pasa por C. Siendo paralelas, esta recta y la recta (AB) forman con la recta (AC) ángulos iguales, codificados en color rojo en la figura de la derecha (ángulos alternos-internos). Del mismo modo, los ángulos codificados en color azul son iguales (ángulos correspondientes). Por otro lado, la suma de los tres ángulos del vértice C es el ángulo llano. Así que la suma de las medidas del ángulo de color rojo, del ángulo verde y del azul es un ángulo de 180° (o π radianes). En conclusión, la suma de los ángulos de un triángulo es 180°.

Esta propiedad es el resultado de la geometría euclidiana. No se verifica en general en la geometría no euclidiana.

Otras propiedades[editar]

• La suma de las longitudes de dos de los lados de un triángulo es siempre mayor que la longitud del tercer lado.

• El valor de la base media de un triángulo (segmento que une dos puntos medios de dos lados) es igual a la mitad del lado paralelo.

• Los triángulos (polígonos de tres lados) son los únicos polígonos siempre convexos, no pueden ser cóncavos, dado que ninguno de sus tres ángulos puede superar los 180 grados o ${\displaystyle \pi }$ radianes.

• Para cualquier triángulo se verifica el Teorema del seno que establece: «Los lados de un triángulo son proporcionales a los senos de los ángulos opuestos»:

${\displaystyle {\frac {a}{\sin(\alpha \,)}}={\frac {b}{\sin(\beta \,)}}={\frac {c}{\sin(\gamma \,)}}}$

• Todo polígono convexo de n lados se puede descomponer en n-2 triángulos con interiores disjuntos, considerando un vértice del cual se trazan n-3 segmentos a los vértices no contiguos.¹¹​

El teorema de Pitágoras gráficamente.

• Para cualquier triángulo se verifica el Teorema del coseno que establece: «El cuadrado de un lado es igual a la suma de los cuadrados de los otros lados menos el doble del producto de estos lados por el coseno del ángulo comprendido»:

${\displaystyle a^{2}=b^{2}+c^{2}-2bc\cdot \cos(\alpha \,)\,}$

${\displaystyle b^{2}=a^{2}+c^{2}-2ac\cdot \cos(\beta \,)\,}$

${\displaystyle c^{2}=a^{2}+b^{2}-2ab\cdot \cos(\gamma \,)\,}$

• Para cualquier triángulo rectángulo, cuyos catetos miden a y b, y cuya hipotenusa mida c, se verifica el Teorema de Pitágoras:

${\displaystyle c^{2}=b^{2}+a^{2}\,}$

De la ecuación anterior se deducen fácilmente 3 fórmulas de aplicación práctica:

${\displaystyle a={\sqrt {c^{2}-b^{2}}}}$

${\displaystyle b={\sqrt {c^{2}-a^{2}}}}$

${\displaystyle c={\sqrt {a^{2}+b^{2}}}}$

• Mediante rotación, traslación, simetría axial y simetría puntual la imagen de un triángulo es un triángulo congruente al propuesto.¹²​
• Dado un triángulo en el plano cartesiano se puede hallar la ecuación de una parábola circunscrita de eje horizontal o vertical ¹³​

Puntos especiales[editar]

Geométricamente se pueden definir varios casos que están ligados a un triángulo en sí o en relación a la posición de una circunferencia.

• Baricentro o Centroide: es el punto que se encuentra en la intersección de las medianas, y equivale al centro de gravedad¹⁴​ ¹⁵​

Razones trigonométricas en triángulos rectángulos[editar]

Artículo principal: Trigonometría

Artículo principal: Función trigonométrica

Un triángulo rectángulo siempre incluye un ángulo de 90° (π/2 radianes), aquí etiquetado C. Los ángulos A y B puede variar. Las funciones trigonométricas especifican las relaciones entre las longitudes de los lados y los ángulos interiores de un triángulo rectángulo.

En triángulos rectángulos, las razones trigonométricas del seno, el coseno y la tangente pueden ser usadas para encontrar los ángulos y las longitudes de lados desconocidos. Los lados del triángulo se denominan como sigue, con respecto a uno de los ángulo agudos:

• La hipotenusa es el lado opuesto al ángulo recto. Es el lado más largo de un triángulo rectángulo.
• El cateto opuesto es el lado opuesto al ángulo agudo considerado.
• El cateto adyacente es el cateto que forma el ángulo agudo considerado.

Seno, coseno y tangente[editar]

El seno de un ángulo es el cociente entre la longitud del cateto opuesto y la longitud de la hipotenusa.

${\displaystyle {\text{sen}}\alpha ={\frac {\color {ForestGreen}{\textrm {opuesto}}}{\color {Red}{\textrm {hipotenusa}}}}={\frac {a}{c}}.}$

El coseno de un ángulo es el cociente entre la longitud del cateto del lado adyacente y la longitud de la hipotenusa.

${\displaystyle \cos \alpha ={\frac {\color {Blue}{\textrm {adyacente}}}{\color {Red}{\textrm {hipotenusa}}}}={\frac {b}{c}}.}$

La tangente de un ángulo es el cociente entre la longitud del cateto opuesto y la longitud del cateto adyacente.

${\displaystyle \tan \alpha ={\frac {\color {ForestGreen}{\textrm {opuesto}}}{\color {Blue}{\textrm {adyacente}}}}={\frac {a}{b}}.}$

Nota: Los cocientes de las tres relaciones anteriores no dependen del tamaño del triángulo rectángulo.

Funciones inversas

Las funciones trigonométricas inversas pueden ser usadas para calcular los ángulos internos de un triángulo rectángulo al tener la longitud de dos lados cualesquiera.

Arcsin (arcoseno) puede ser usado para calcular un ángulo con la longitud del cateto opuesto y la de la hipotenusa.

${\displaystyle \theta =\arcsin \left({\frac {\color {ForestGreen}{\textrm {opuesto}}}{\color {Red}{\textrm {hipotenusa}}}}\right)}$

Arccos (arcocoseno) puede ser usado para calcular un ángulo con la longitud del cateto adyacente y la de la hipotenusa.

${\displaystyle \theta =\arccos \left({\frac {\color {Blue}{\textrm {adyacente}}}{\color {Red}{\textrm {hipotenusa}}}}\right)}$

Arctan (arcotangente) puede ser usada para calcular un ángulo con la longitud del cateto opuesto y la del cateto adyacente.

${\displaystyle \theta =\arctan \left({\frac {\color {ForestGreen}{\textrm {opuesto}}}{\color {Blue}{\textrm {adyacente}}}}\right)}$

En los cursos introductorios de geometría y trigonometría, la notación sin⁻¹, cos⁻¹, etc., es frecuentemente utilizada en lugar de arcsin, arccos, etc. Sin embargo, la notación de arcsin, arccos, etc., es estándar en matemáticas superiores donde las funciones trigonométricas son comúnmente elevadas a potencias, pues esto evita la confusión entre el inverso multiplicativo y la función inversa

Cuadrilátero

Clases de cuadriláteros convexos.

En geometría plana, un cuadrilátero o tetrágono es un polígono de cuatro lados y cuatro vértices

La palabra "cuadrilátero" procede de dos palabras latinas quadri, que significa cuatro, y latus, que significa lado.

Los cuadriláteros según su forma se dividen en complejos y simples, y estos a su vez se dividen en cóncavos y convexos, y estos a su vez pueden estar o no inscritos o circunscritos.

Propiedades

• Los cuadriláteros tienen dos diagonales.
• Las diagonales de un cuadrilátero se cortan si y solamente si es convexo.
• La suma de la medida de los ángulos de un cuadrilátero ${\displaystyle ABCD}$ convexo es 360º o 2π radianes.

${\displaystyle \angle A+\angle B+\angle C+\angle D=360^{\circ }}$

• Todo cuadrilátero simple puede expresarse como la unión de dos triángulos con lado común que es una de las diagonales.
• En un cuadrilátero inscrito en una circunferencia la suma de la medida de sus ángulos opuestos es igual a 180º.

• Sea ABCD un cuadrilátero inscrito en una circunferencia de diámetro ${\displaystyle AB}$, entonces las proyecciones de los lados AD y BC sobre la recta CD son iguales.¹​
• El área de un cuadrilátero inscrito se obtiene con la fórmula ${\displaystyle A={\sqrt {(p-a)(p-b)(p-c)(p-d)}}}$ donde a, b, c, d son los lados y p es el semiperímetro.
• Si 2α es la suma de dos ángulos opuestos de un cuadrilátero circunscrito, A su área, a,b, c, d sus lados entonces cabe la fórmula A² = (abcd)sen²α.²​
• Si las diagonales de un cuadrilátero convexo lo divide en cuatro triángulos y los radios de la circunferencias inscritas en estos triángulos son iguales, entonces dicho cuadrilátero es un rombo.
• Si se unen con cuatro segmentos los puntos medios de todos los lados de un cuadrilátero, entonces dichos segmentos forman un paralelogramo.
• Si en el cuadrilátero ABCD los radios de las circunferencias inscritas en los triángulos ABC, BCD, CDA, DAB son iguales, entonces dicho cuadrilátero es un rectángulo.
• Si las diagonales de un cuadrilátero lo dividen en cuatro triángulos de igual perímetro, entonces el cuadrilátero original es un rombo.³​
• Si un cuadrilátero está circunscrito entonces la suma de sus lados opuestos con iguales. ${\displaystyle AB+CD=BC+DA}$.⁴​
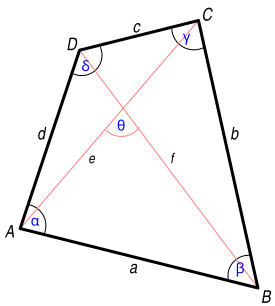
• Para un cuadrilátero convexo se cumple ${\displaystyle a^{2}+b^{2}+c^{2}+d^{2}=d_{1}^{2}+d_{2}^{2}+4m^{2}}$ donde ${\displaystyle a,b,c,d}$ son los lados; ${\displaystyle d_{1},d_{2}}$,las diagonales y m, la longitud del segmento que une los puntos medios de las diagonales.
• También se verifica: ${\displaystyle d_{1}^{2}+d_{2}^{2}=m_{1}^{2}+m_{2}^{2}}$ donde ${\displaystyle d_{1},d_{2}}$ son las diagonales y ${\displaystyle m_{1},m_{2}}$ son los segmentos que unen los puntos medios de lados opuestos.⁵​

Elementos de un cuadrilátero

Los elementos de un cuadrilátero son los siguientes:

• 4 vértices: puntos de intersección de los lados que conforman el cuadrilátero.

• 4 lados: segmentos que unen los vértices contiguos.

• 2 diagonales: segmentos cuyos extremos son dos vértices no contiguos.

• 4 ángulos interiores: el determinado por dos lados contiguos.

• 4 ángulos exteriores: el determinado por la prolongación de uno de los lados sobre un vértice y el contiguo en el mismo vértice.

Clasificación de los cuadriláteros

Deltoides

Tipos de Paralelogramos

Los cuadriláteros se clasifican según el paralelismo de sus lados, sus longitudes y sus ángulos interiores:

• Paralelogramo: sus lados opuestos son paralelos.
• Cuadrado: todos sus lados son iguales, todos sus ángulos interiores son rectos, sus diagonales son iguales y perpendiculares entre si, tiene una circunferencia inscritas y otra circunscrita.
• Rombo: todos sus lados son iguales, cada par de ángulos agudos y obtusos son opuestos, sus diagonales son distintas y perpendiculares entre sí, son bisectrices, tiene una circunferencia inscrita.
• Rectángulo: sus lados opuestos son iguales dos a dos y los paralelos, todos sus ángulos interiores son rectos, sus dos diagonales son iguales pero no son perpendiculares entre si y tiene una circunferencia circunscrita.
• Romboide: sus lados opuestos son iguales dos a dos, cada par de ángulos agudos y obtusos son opuestos, sus dos diagonales son de distinta longitud y no son perpendiculares entre sí.
• Trapecios: En geometría, se llama trapecio a un cuadrilátero que tiene dos lados no consecutivos paralelos llamados bases del trapecio, y el segmento perpendicular entre las dos bases y su propia longitud son llamadas altura del trapecio
• Trapezoides: En geometría euclídea plana, un trapezoide es un cuadrilátero convexo sin lados paralelos.

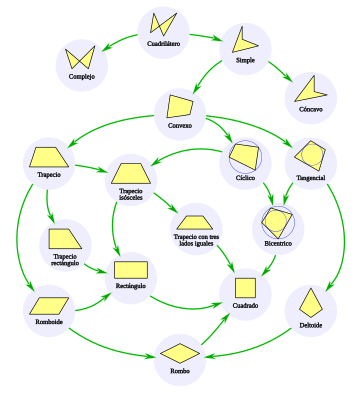
Taxonomía de los cuadriláteros

En el gráfico ilustrativo de la taxonomía de los cuadriláteros se pasa de las definiciones más generales a las más específicas siguiendo el sentido de las flechas.

Así se parte de un cuadrilátero definido como un polígono cerrado de cuatro lados, sin más restricciones, para diferenciar los cuadriláteros compuestos de los simples.

En un cuadrilátero complejo, dos de sus lados se cortan. En uno simple los lados no se cruzan.

Los cuadriláteros simples se dividen en:

• Cóncavos. En un cuadrilátero cóncavo al menos uno de sus ángulos interiores mide más de 180°.
• Convexos. Un cuadrilátero convexo no tiene ángulos interiores que midan más de 180°. Los convexos se subdividen en:

1. Cuadrilátero cíclico, si se puede trazar una circunferencia que pase por sus vértices.
2. Cuadrilátero tangencial, si se puede trazar una circunferencia tangente a cada uno de sus lados.
3. Trapecios, si tienen dos lados paralelos. Se diferencian:
   1. Romboide, como caso más general de paralelogramo, si los lados son paralelos dos a dos.
   2. Trapecio rectángulo, que tiene un lado perpendicular a sus bases.
   3. Trapecio isósceles, cuyos lados no paralelos son de igual medida. Este trapecio también es cíclico.

A un cuadrilátero que al mismo tiempo sea cíclico y tangencial se le denomina cuadrilátero bicéntrico. El deltoide es tangencial con dos pares de lados iguales.

Un caso particular de trapecio isósceles es cuando la longitud de una de las bases es igual que la de sus lados, por lo cual se configura un trapecio de tres lados iguales.

Cuadrilátero simétrico

Se llama así cualquier cuadrilátero en el cual una de sus diagonales sirve de eje de simetría. Por ejemplo: el rombo, el deltoide, el cuadrado.

El rectángulo es un cuadrilátero que simultáneamente cumple las características de:

• Paralelogramo, al ser paralelos sus lados opuestos.
• Trapecio rectángulo, porque los lados son perpendiculares a las bases.
• Trapecio isósceles, por ser de igual longitud los lados que no constituyen las bases.

Del mismo modo se puede verificar que el rombo es un deltoide paralelogramo, pues cumple las características de ambos.

Por último, el cuadrado puede considerarse rombo, rectángulo, con lados iguales y bicéntrico.

Fórmulas

Los cuatro lados de un cuadrilátero: a, b, c, d ;

los cuatro vértices: A, B, C, D ;

las dos diagonales: e, f.

• La suma de los ángulos internos es igual a 360°:

${\displaystyle \alpha +\beta +\gamma +\delta =360^{\circ }}$

• Si las diagonales son perpendiculares, ocurre la relación siguiente:

${\displaystyle \theta =90^{\circ }\Longleftrightarrow a^{2}+c^{2}=b^{2}+d^{2}}$

• El área de un cuadrilátero se puede calcular mediante cualquiera de estas seis fórmulas:

${\displaystyle A={\frac {ef\sin \theta }{2}}}$ ${\displaystyle A={\frac {ad\sin \alpha +bc\sin \gamma }{2}}={\frac {ab\sin \beta +cd\sin \delta }{2}}}$ ${\displaystyle A={\frac {1}{4}}\left(b^{2}+d^{2}-a^{2}-c^{2}\right)\tan \theta }$ ${\displaystyle A={\frac {1}{4}}{\sqrt {4e^{2}f^{2}-\left(b^{2}+d^{2}-a^{2}-c^{2}\right)^{2}}}}$ ${\displaystyle A={\frac {1}{2}}{\sqrt {|{\vec {e}}|^{2}|{\vec {f}}|^{2}-({\vec {e}}\cdot {\vec {f}})^{2}}}}$

${\displaystyle A={\tfrac {1}{2}}ad\cdot \sin {\alpha }+{\tfrac {1}{4}}{\sqrt {4b^{2}c^{2}-(b^{2}+c^{2}-a^{2}-d^{2}+2ad\cdot \cos {\alpha })^{2}}}}$ (para un cuadrilátero con concavidad en C cambiar el primer signo + por -).

Cuadriláteros inscriptos

Son aquellos cuyos vértices están en una circunferencia y sus lados son cuerdas. Se establecen las siguientes fórmulas siendo

sus lados a,b,c d; y sus diagonales d₁, d₂

${\displaystyle d_{1}d_{2}=ac+bd}$

${\displaystyle {\frac {d_{1}}{d_{2}}}={\frac {ad+bc}{ab+cd}}}$

${\displaystyle d_{1}={\sqrt {\frac {(ad+bc)(ac+bd)}{ab+cd}}}}$

${\displaystyle d_{2}={\sqrt {\frac {(ab+cd)(ac+bd)}{ad+bc}}}}$

​

Teorema de Arquímedes-Faure

Sea el cuadrilátero inscrito de lados a,b,c,d; de diagonales perpendiculares que al intersecarse determinan los segmentos m,n en uno de ellos y p, q en el otro, R radio de la circunferencia circunscrita. En tal caso son válidas las igualdades:

${\displaystyle a^{2}+c^{2}=b^{2}+d^{2}=4R^{2}}$

Ejercicios

 Perímetro y Área de Polígonos

En primer lugar veremos lo relacionado con los polígonos.

El perímetro de un polígono es igual a la suma de las longitudes de sus lados y su área es la medida de la región o superficie encerrada por un polígono.

 

 Área y perímetro del triángulo

- Cálculo del perímetro

Es la longitud de su contorno ó la suma de sus lados.

P = a + b + c

 

Recuerda:

- El perímetro de un triángulo escaleno (todos los lados distinta medida) de lados a, b y c se puede calcular utilizando la siguiente fórmula:

P = a + b + c

- El perímetro de un triángulo isósceles (dos lados igual medida) de lados a y base b se puede calcular utilizando la siguiente fórmula:

P = a + a + b, es decir,

P = 2 • a + b

- El perímetro de un triángulo equilátero (todos los lados igual medida)  de lado a se puede calcular utilizando la siguiente fórmula:

P = a + a + a, es decir,

P = 3 • a

- Cálculo del área

Es el producto de uno de sus lados por la altura correspondiente a él, dividido por dos.

3- Área y perímetro del cuadrado

- Cálculo del perímetro

Es la longitud de su contorno ó la suma de sus lados

P = a + a + a + a, es decir,

P = 4 • a

- Cálculo del área

Para calcular el área de un cuadrado multiplicaremos su base por su altura, es decir, su largo por su ancho.

A = lado x lado = lado²

A = a • a

A = a²

4- Área y perímetro del rectángulo

- Cálculo del perímetro

Es la longitud de su contorno ó la suma de sus lados

 

P = a + a + b + b, es decir,

P = 2 • a + 2 • b

P = 2 • (a + b) 

- Cálculo del área

Para calcular el área de un rectángulo multiplicaremos su base por su altura, es decir, su largo por su ancho.

A = base x altura.

A = a • b

5- Área y perímetro del romboide

El perímetro del romboide es igual a la suma de las longitudes de sus cuatro lados.

P = 2 • a + 2 • b

P = 2 • (a + b)

- Cálculo del área

Se obtiene a partir del área del rectángulo, multiplicando la base por la altura del romboide (no por el otro lado).

A = base x altura

6-  Área y perímetro del rombo

- Cálculo del área

Para calcular el área del rombo, recuerda que éste es un cuadrilátero con cuatro lados iguales, paralelos dos a dos.

Si unimos los vértices opuestos, obtenemos su diagonal mayor (la que mide más) y su diagonal menor (la que mide menos).

 

El área del rombo resultará de multiplicar su diagonal mayor por su diagonal menor y dividirlo por dos.

.

- Cálculo del perímetro

Sumando las longitudes de los lados de un polígono hallaremos su perímetro.

¿Cómo calculo  el perímetro si sólo tengo el valor de las diagonales del rombo?

En la figura de arriba, aparece un triángulo coloreado en verde. Ese triángulo está formado por un cateto o lado que es la mitad de la diagonal mayor (D/2), otro cateto o lado que es la mitad de la diagonal menor (d/2) y por la hipotenusa (a), que es a su vez lado del rombo.

Entonces, recordemos, para aplicarlo, el Teorema de Pitágoras:

a² = b² + c²

Entonces, si reemplazamos los valores tendremos:

Donde:

D = diagonal mayor

d = diagonal menor

a = lado

Recuerda ⇒ Los lados del rombo son iguales. Entonces si por ejemplo el resultado del lado es 6 cm, el perímetro será 6 + 6 + 6 + 6 = 24cm

7- Áreas y perímetros  de polígonos regulares 

- Cálculo del perímetro

Sumando las longitudes de los lados de un polígono hallaremos su perímetro.

- Cálculo del área

Para calcular el área de un polígono regular cualquiera se divide en triángulos uniendo el centro con cada uno de los vértices. La altura de cada uno de los triángulos coincide con la apotema del polígono. Se calcula el área de uno de estos triángulos y se multiplica por el número de triángulos que se han formado.

n= número de lados

Perímetro = número de lados multiplicado por longitud del lado.

El área de un polígono regular es igual al producto de su perímetro por su apotema dividido entre dos.

Apotema: segmento que une el centro del polígono con el punto medio de cada lado.

Esta fórmula permite calcular la apotema de cualquier polígono regular.

Ejercicios

 La circunferencia y el círculo

La circunferencia es una línea curva cerrada y plana cuyos puntos están a igual distancia de otro fijo, llamado centro. Para dibujar circunferencias utilizamos el compás.

 

Ejemplos de circunferencia: anillo, aro.

 Círculo

Es una figura plana limitada por una circunferencia. Está formado por la circunferencia y la parte de plano que hay dentro de ella.

 

Ejemplos de círculo: moneda, disco

Elementos de la circunferencia y el círculo:

- Centro: punto del cual equidistan todos los puntos que forman la circunferencia.

 

- Radio: segmento que une el centro con un punto cualquiera de la circunferencia.

 

 

- Cuerda: segmento que une dos puntos cualesquiera de la circunferencia.

 

- Diámetro: cuerda que pasa por el centro y equivale a dos radios.  Por lo tanto, el diámetro = 2 x radio.

 

- Arco: parte de la circunferencia comprendida entre dos puntos cualesquiera.

- Semicircunferencia: arco igual a la mitad de la circunferencia. 

Su longitud es aproximadamente 3,14 veces la medida de su diámetro (L = 3,14 X d).

Posiciones de una recta respecto a una circunferencia

- Recta exterior a una circunferencia: no tienen ningún punto en común. La distancia del centro a la recta es mayor que el radio.

- Recta tangente a una circunferencia: tienen un punto en común. La distancia del centro a la recta es igual al radio.

 Recta secante a una circunferencia: tienen dos puntos en común (la corta). La distancia del centro a la recta es menor que el radio.

 

 

Figuras circulares

- Semicírculo: cada una de las mitades de un círculo que resulta al trazar un diámetro. El diámetro divide a la circunferencia y al círculo en dos partes iguales que se llaman respectivamente semicircunferencias y semicírculos. Recuerda que dos circunferencias concéntricas son las que tienen el mismo centro.

- Sector circular: parte del círculo limitada por dos radios y su arco correspondiente.

- Segmento circular: parte del círculo limitada por una cuerda y su arco correspondiente.

- Corona circular: parte del círculo comprendida entre dos circunferencias que tienen el mismo centro.

Ejercicios

Los mejores cursos GRATIS

Ver TODOS los 1585 cursos GRATIS

Participa en el Foro y los Chats

El Círculo y las figuras circulares

El círculo es la superficie del plano delimitada por una circunferencia.

Las partes de un círculo se denominan figuras circulares:

Sector circular: Es aquella parte del círculo delimitada por dos radios y el arco que delimitan.

Segmento circular: Es aquella parte del círculo delimitada por una cuerda y el arco que delimita.

Corona circular: es la parte del círculo delimitado entre una circunferencia y una circunferencia interior concéntrica.

Trapecio circular: es la parte de la corona circular delimitada por 2 radios.